浮点数

计算机如何用二进制表示浮点数？为何0.1+0.1不等于0.2？

上一节课，我们讲了整型数的表示方法：补码，今天我们讲讲浮点数的表示方法。浮点数在平时的开发中也经常用到，比如用来表示金额等。浮点数并不能精确地表示整数或小数，所以，在使用时，要多加小心，稍有不慎就会引入bug。因此，了解浮点数的表示方法等相关理论知识，就相当有必要了。

一、实数的二进制科学记数法

浮点数是计算机中用来表示实数的数据类型。实数是一个数学概念，这里我们可以简单理解为小数。不过，整数也可以看做实数，比如5可以看做5.0，也算是实数。

我们知道，整数在计算机中有固定的表示方法（或者叫存储格式）：补码，同样，浮点数也有固定的表示方法，并且形成了一份规范文件，叫做IEEE754标准。绝大多数计算机都参照这个标准来存储浮点数。

浮点数在计算机中的存储格式类似科学记数法，所以，我们先来了解一下什么是科学记数法。

在数学计算中，特别是在表示一些物理量时，比如星球之间的距离，为了方便表示很大很大的数，我们一般采用科学记数法。我们将数据表示成x*10^{y的形式，x叫做尾数或有效数字，y叫做指数、幂或者阶数。例如，我们可以将12350000表示为1.235*10}7^{。为了方便书写，我们一般会将科学记数法的表示形式，简化为xEy的形式。例如，我们把1.235*10}7简写为1.235E7。在编程中，我们也可以使用这种简化的书写方式。示例代码如下所示。

float f1 = 100000000.0f;
System.out.println("" + f1); //输出1.0E8
float f2 = 1.3E23f;
System.out.println("" + f2); //输出1.3E23

上面讲的是十进制的科学记数法，接下来，我们再看一下二进制的科学记数法。

对于一个实数，我们可以将其分为两部分：整数部分和小数部分。我们将整数部分和小数部分分别转换为二进制数，然后中间用点号（.）连接，就得到了实数对应的二进制表示。例如，十进制数12.375转换成二进制表示为：1100.011，十进制数-12.375转换成二进制表示为：-1100.011。

对于整数如何转化成二进制表示，我们在上一节课中已经讲过了，采用是除2求余的方法。接下来，我们重点讲一下，如何将小数部分转换成二进制表示。

对于小数的十进制表示，点号以后的每一位都对应一个权值，依次为1/10，1/10^2，1/103...以此类推。同理，对于小数的二进制表示，点号以后的每一位对应权值依次为1/2，1/2^2，1/23...以此类推。

类比十进制的乘10运算，假设某个小数w表示成二进制数之后为：0.xyz（x、y、z为0或1），将其乘2就相当于点号后移一位，变为：x.yz，这时对其取整，就得到了x，这样我们就分离出了第一位小数。以此类推，每次乘以2，然后取整，就能依次得到小数点后的每一位。这种将小数转换为二进制表示的方法叫做乘2取整法。下图是对于上述处理过程的举例解释。

6-1.png

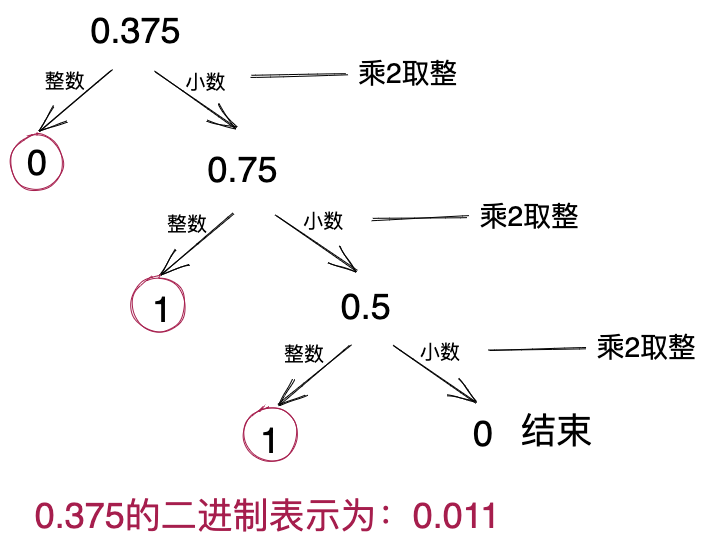
但是，上述实数的二进制表示中包含负号和点号，只适合人类阅读，还无法直接存储到计算机中。那么，怎么将类似-1100.011这样的二进制格式，转换为适合计算机存储的二进制格式呢？换句话说，如果我们用4字节去存储实数，那么如何将类似-1100.011这样的二进制串的所有信息，都保存在这4个字节中呢？

二、实数的存储格式：定点数

借鉴上一节课处理整数符号的方法，我们将一串二进制位的最高位作为符号位，来表示正负。符号位为0表示正数，符号位为1表示负数。符号如何存储的问题解决了。接下来，我们来看如何存储点号，也就是，当把二进制位存储到4个字节中时，如何区分哪几位是整数部分，哪几位是小数部分。比较简单的方法是固定整数和小数所占二进制位的个数，比如最高位为符号位，接下来的20位表示整数，最后11位表示小数。如下图所示。

6-2.png

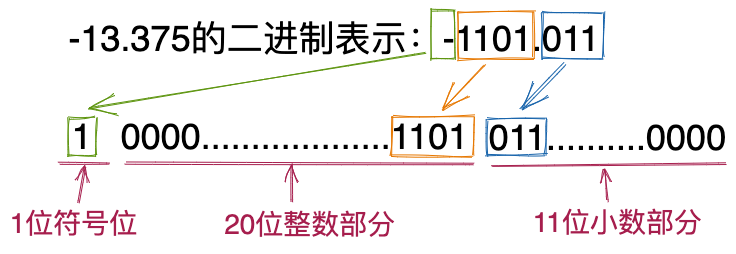
以上实数在计算机中的表示方法叫做定点数表示法，也就是说点号在整数和小数之间的位置是固定的。定点数最大的问题是，有时候会浪费一些存储空间。比如，当我们表示一个只包含整数部分，不包含小数部分的实数时，也就是说，小数部分的二进制位都为0，即便整数部分都要溢出了，但也不能挪用小数部分的二进制位。同理，当我们要表示一个高精度的实数，并且它只包含小数不包含整数时，也就是整数部分的二进制位都是0，即便小数部分因为存储空间不够都要被截断了，但也不能挪用整数部分的二进制位。

三、实数的存储格式：浮点数

为了有效利用存储空间，于是就发明了浮点数，顾名思义，点号在32个二进制位中的位置是不固定的，这样就充分利用存储空间，能够表示更大的数据范围和更高的小数精度。

计算机中的浮点数一般分为4字节单精度浮点数和8字节双精度浮点数，对应到Java语言中就是float类型和double类型。根据IEEE754标准的规定，浮点数的二进制表示格式为：(-1)^s*M*2E。实际上就是二进制的科学记数法。(-1)^{s表示符号，s为0时表示正数，s为1时表示负数。M是有效数字或尾数，E是指数、幂或阶数。例如，-12.375表示成二进制为-1100.011，进而表示成二进制科学记数法为(-1)}11.1000112^{3，当然也可以表示为(-1)}111.000112^2等。

为了统一表示方式，IEEE754标准规定，M的整数位必须是1，即M必须大于等于1且小于2。这样-12.375就只能表示为(-1)^1*1.100011*23，对应的S为1，M为1.00011，E为3。那么，如何将二进制科学记数法存储在计算机中呢？

IEEE754标准规定，对于4字节单精度浮点数，最高位存储s，中间8位存储指数E，叫做指数域，最后23位存储有效数字，叫做有效数字域。对于8字节的双精度浮点数，最高位存储s，中间11为存储指数E，最后52为存储有效数字。因为这两种浮点数的存储结构类似，我们拿单精度浮点数来举例讲解。

6-3.png

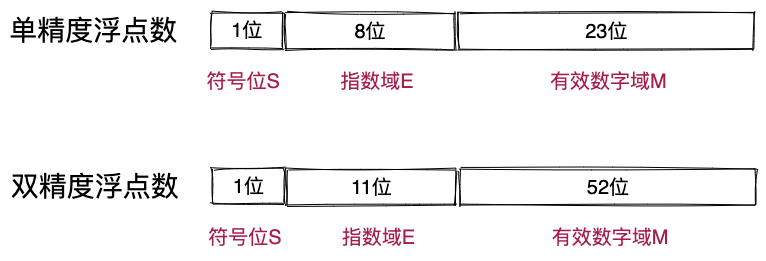
对于M和E的存储格式，IEEE754标准还有其他规定。

因为IEEE754标准规定，M的整数位必须是1，所以，在存储M时，我们可以不用存储整数位1，只存储小数位即可。也就是说，我们可以用23个二进制位存储24位有效数字。

我们再来看指数E如何存储。E是一个整数，它既可以是负数（比如0.000011用科学记数法表示为1.1*2^(-5)，E为-5），也可以是正数。整数的存储方法有多种，上一节讲到原码和补码。用原码存储，8个二进制位可以表示的范围是[-127, 127]，用补码存储，8位二进制位可以表示的范围是[-128, 127]。不过，IEEE754并没有沿用原码或补码来存储E（当然，使用原码或补码也是可以的）。

IEEE754限定指数E的范围是[-126, 127]，具体为什么是这个范围，我们待会再解释。IEEE754将指数域解释为无符号类型，也就是，指数域中没有符号位，8个二进制位全是数值位，那么，指数域可表示数据范围是[0, 255]（0000 0000 ~ 1111 1111）。不过，这样，负数指数就无法存储在指数域了。为了解决这个问题，IEEE标准将指数E统一加127之后，再存储到指数域，同理，当从指数域中取出指数时，也要对应的减去127。这样，指数E加127之后，范围就变成了[1, 254]，正好落在指数域可表示的范围（[0, 255]）内。我们举个例子，如下图所示。

6-4.png

你可能会说，指数域中的0和255岂不是没用到。如果IEEE754将指数E范围扩大一点，限定为[-127, 128]，那么加127之后，范围变成[0, 255]，这不就正好跟指数域可表示范围相吻合，就不浪费0和255两个值了。实际上，IEEEE754之所以把指数E的数据范围限定为[-126, 127]，这是因为指数域中的0和255这两个值还有其他特殊用处。我们依次来看下。

1）指数域为0（0000 0000）用来辅助表示浮点数0。

前面讲过，IEEE规定有效数字M的整数位为1，并且在存储到有效数字域中时，将整数位1省略。反过来，从有效数字域中的读取的二进制位，前面加1才是真正的有效数字。有效数字域能表示的最小数为000....00000（23个0），将其翻译为有效数字时，在前面加1变为：1000...00000（1个1，23），所以，有效数字域无法表示为0的有效数字，也就无法表示浮点数0了。

为了表示浮点数0，IEEE754标准规定，当指数域为0时，从有效数字域中读取的二进制位不需要在前面加1。这样，当指数域为0，有效数字域为0时，就可以表示浮点数0了。

看到这里，你可能会说，IEEE754真复杂。是的，这可是Intel公司请当时最优秀的数值分析家之一William Kahan 教授设计的。

2）指数域为255（1111 1111）用来辅助表示无穷大或NaN。

当指数域为255，有效数字域为0时，表示正无穷（s为0）和负无穷大（s为1）。当指数域为255，有效数字域的二进制位不全为0时，表示这是一个无意义数NaN（Not a Number）。在Java中的Float类中定义3个静态常量来表示正负无穷大和NaN，如下代码所示。当我们在开发中，需要初始化某个浮点类型的变量为正无穷大或负无穷大时，可以直接使用以下静态常量。

public static final float POSITIVE_INFINITY = 1.0f / 0.0f;
public static final float NEGATIVE_INFINITY = -1.0f / 0.0f;
public static final float NaN = 0.0f / 0.0f;

四、浮点数的表示范围和精度

浮点数的存储格式讲清楚了，我们再来看一下浮点数的表示范围和精度问题。

1）浮点数的表示范围

确定浮点数的表示范围，也就是找到其可以表示的最大值和最小值。我们还是拿4字节的单精度浮点数来举例讲解。

在IEEE754标准规定的浮点数的存储结构中，有效数字域占23个二进制位，所以，有效数字M的最大值是1.111...11（总共有24个1）。指数的范围是[-126, 127]，所以，指数的最大值是127。因此浮点数可以表示的最大值是1.111...11 * 2^{127，最小值是-1.111...11*2}127。转化成十进制数约等于3.4E38和-3.4E38。

浮点数可以表示的范围是非常大的。而同样占用4个字节存储空间的int类型的表示范围只有-2^32~232-1，也就是-1073741824~1073741823。那你有没有想过，同样是4字节长度，为什么浮点数就可以表示这么大的范围呢？

之所以浮点数能表示这么大的范围，是因为它有选择地表示这个范围内的一部分的数，而非全部的数。一来，实数是无限多的，全部表示本身就是不可能的事，二来，根据排列组合，32个二进制位可以最多表示2^{32个不同的数。根据鸽巢原理，用2}32个数来表示无限多的实数，必然会有取舍。由此我们也可以得到：不同的实数，在用浮点数表示的时候，在计算机中存储的可能是相同的浮点数。

2）浮点数的精度问题

当某个实数表示成二进制科学计数法，其有效数字位数超过24位时，就会做精度舍弃，类似四舍五入的方法舍弃多出来的有效数字（注意不是直接截断舍弃，具体舍入的算法比较复杂，我们就不展开讲解了）。由此就会产生精度问题。某个实数存入计算机中，再次被取出时，有可能就不是之前存入的实数值了。

这里需要注意一下，不仅仅只有小数会有精度问题，整数也有精度问题。只要有效数字个数超过24个，就会存在精度问题。示例代码如下所示。

float f = 33554433.0f;
System.out.println(f); //输出结果：3.3554432E7

了解了精度问题产生的原因之后，我们来看下面这段代码，请你思考下，这段代码的打印结果是什么？

float f = 0.1f;
System.out.printf("%.11f\n", f6);//格式化输出，保留11位小数

你可能会说，0.1的小数位只有1位，转化成二进制之后，有效数字肯定小于24个，所以，0.1肯定能准确表示，打印结果是0.1。

实际上，这样的分析是不对的，浮点数0.1在计算机中无法精确表示，因为十进制的0.1换算成二进制是一个无限循环小数，有效数字位数无穷多，如下图所示。有效数字舍入处理之后，最终打印的结果0.10000000149（注意，代码中使用printf()保留11位小数，如果使用println()打印，会舍入显示为0.1）。这个值大于0.1，也应证了我们前面讲到的，有效数字个数大于24时，执行舍入操作，而非直接截断。因为如果是直接截断的话，最终的值会小于0.1，而舍入的话，就有可能大于0.1。

6-5.png

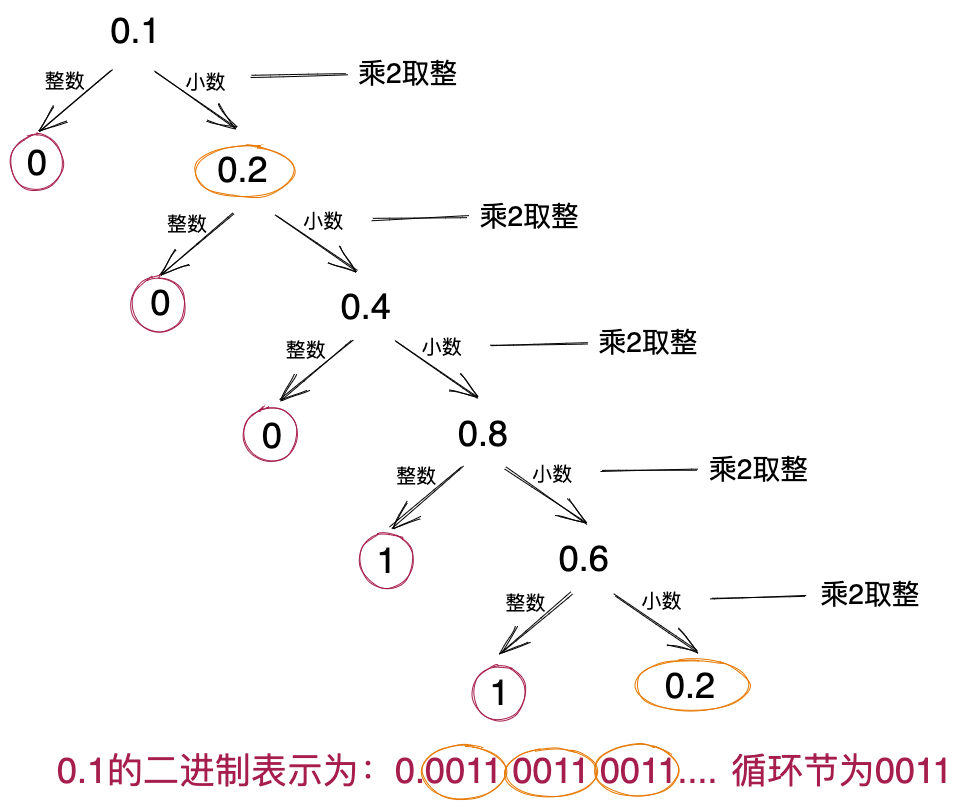
五、浮点数的替代品：BigDecimal

浮点数的表示会存在误差，因此浮点数的计算也会存在误差，如下所示。不过，这个误差非常小，大部分对精度不是特别敏感的系统，用浮点数来表示实数就足够了。

float f1 = 10.00f;
float f2 = 9.60f;
float f3 = f1 - f2;
System.out.println(f3); //输出0.39999962

对精度比较敏感的金融系统，代码中充斥着各种浮点数的表示和计算，一丢丢误差累积下来就会产生比较大的误差，所以，金融系统一般采用BigDecimal来表示实数。BigDecimal将整数部分和小数部分分开存储，小数部分也当做整数来存储，这样就能精确表示像0.1这样数据了。如下所示。

BigDecimal bg = new BigDecimal("0.1");
System.out.println(bg.toString()); //输出0.1

注意上述代码，传递进BigDecimal中的是字符串“0.1”，而非float类型数据0.1f，否则BigDecimal将无法表示精确的0.1，原因是0.1在传入BigDecimal之前已经是不准确的了。如下代码所示。

BigDecimal bg = new BigDecimal(0.1f);
System.out.println(bg.toString());//输出0.100000001490116119384765625

BigDecimal还提供了相应的方法，进行精确的加减乘除操作，示例代码如下所示。注意，对于无法整除的除法操作，我们需要指明舍入（Rounding）方法，否则，将抛出ArithmeticException异常。

BigDecimal bg1 = new BigDecimal("10.00");
BigDecimal bg2 = new BigDecimal("9.60");
BigDecimal bg3 = bg1.subtract(bg2);
System.out.println(bg3.toString());

BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("3.0");
BigDecimal c = a.divide(b, 2, BigDecimal.ROUND_HALF_EVEN);

除此之外，浮点数的关系操作（判等、大于、小于等）是比较复杂的，需要引入误差，示例如下所示。而BigDecimal完全不存在这个问题，有现成的方法可以使用。

//浮点数判等，误差小于0.0001就表示f1 == f2
if (Math.abs(f1-f2)<0.0001) {
  ...
 }

//BigDecimal比较，ret=-1,0,1分别表示bg1小于、等于、大于bg2
int ret = bg1.compareTo(bg2);

BigDecimal类提供的方法还有很多，我们就不一一介绍了，你可以自行研究一下。

六、浮点数的精度取舍方法

上面讲了BigDecimal能精确表示和计算实数，但这并不代表就不存在精度舍入问题。存储、显示以及一些具体的业务需要，都有可能需要我们做一些舍入操作。

拿金融系统来举例。在金融系统里面，代码中浮点计算的结果，最好尽量多保留几位小数，在存入数据库或者展示给用户时，再按照业务需要做舍入。比如计算过程浮点数保留8位小数，存入数据库中时保留5位小数，展示给用户时保留2位小数，也就是精确到“分”即可。

常用的舍入算法是四舍五入法，但是，它的累积误差比较大。如果我们通过四舍五入保留1位小数，那么，0.01舍，会产生-0.01的误差，而0.09入，会抵消0.01产生的-0.01的误差。同样，0.02舍和0.08入，0.03舍和0.07入，0.04舍和0.06入，累积下来，都可以实现正负误差相抵。而0.05入，产生+0.05的误差，无人抵消。所以，在数据分布比较均匀的情况下，对于求和操作，10次舍入就会产生一个+0.05的误差。对于金融系统来说，浮点计算非常频繁，100万次舍入操作，就会产生5万的误差。累积误差就比较大了。

金融系统经常用到的舍入方法是四舍六入五成双，也叫做银行家舍入算法，此舍入算法是对四舍五入方法的改进。舍去位的数值小于5时，直接舍去；舍去位的数值大于5时，进位；当舍去位的数值等于5时，根据5前一位数的奇偶性来判断是否需要进位，偶数进位，奇数舍去。举例如下图所示。

6-6.png

当然银行家算法也不是适应用所有的情况，有时候还会根据业务需求选择其他舍入方法，比如分息向上取整，罚息向下取整，以保证客户不亏。实际上，BigDecimal提供了各种舍入算法，以支持各种业务需求，你可以自己去了解下。

除此之外，在开发中，我们要避免依赖数据库的舍入算法。Mysql中Decimal和Oracle中的Number经常用来存储高精度数据，比如Decimal(7,3)和Number(7, 3)，其中，7表示全部的数据位数，3表示小数点之后的数据位数。如果存储的数据超出了字段可表示的精度，Mysql会四舍五入，Oracle会直接截断。为了避免产生不可预测的结果，在存入数据库之前，最好按业务对精度的要求，提前做精度舍入，以免触发数据库的精度舍入。从数据库取出数据时，实数也要用BigDecimal来映射，避免映射为浮点数而导致的精确性问题。

七、课后思考题

1）4字节单精度浮点数能否准确表示int能表示的所有整数呢？如果不能，那么哪个范围内的整数可以准确表示？

2）浮点数可以表示的最小的正数是多少？