位运算
位运算
位运算:>>>和>>有何区别?(原码/反码/补码、算术位移/逻辑位移)
在开始学习本节的内容之前,我们先来看一段代码,如下所示,其中countOneBits()函数用来统计num在计算机中表示为二进制之后,为1的二进制位的个数。仔细分析下面的代码,你觉得这段代码的运行结果是什么?
public class Demo5_1 {
public static void main(String[] args) {
int count = countOneBits(-3);
System.out.println(count);
}
public static int countOneBits(int num) {
int count = 0;
while (num != 0) {
if ((num & 1) == 1) count++;
num >>= 1;
}
return count;
}
}
上述代码会一直执行while循环,不结束,这是为什么呢?如果我们把代码中的>>改为>>>便可以顺利退出while循环,打印结果为31,这又是为什么?代码看似简单,但要想正确分析运行结果,需要我们具有夯实的底层基本功,带着这个问题,我们就来学习本节的内容:整数在计算机中的二进制表示法以及位运算。
一、如何将十进制数转换为二进制数
人类习惯用十进制来计数,逢十进一,这跟人类有十根手指有很大关系。而计算机采用二进制来计数,逢二进一,这跟计算机的硬件电路实现有很大关系。在了解整数在计算机中如何存储的之前,我们先来了解一下二进制数。
十进制表示法用一串数字表表示一个整数。左边叫做高位,右边为低位。每一位只能是0到9之间的数字,并且每一位对应一个权值。权值为10k,最低位的权值为1(100),第二位是101,以此类推,从低位到高位,权值依次乘10。我们把每一位数字跟权值相乘的结果加起来,就是最终要表示的十进制数。二进制的表示法跟十进制表示法类似,区别在于每一位只允许是0或1,每位的权值是2k,从低位到高位,权值依次为1、2、22、23...以此类推。如下图所示。
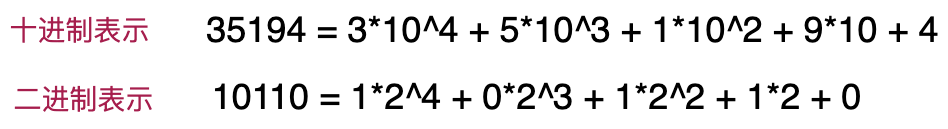
抛开计算机来看,我们人类是如何将一个十进制数转换为二进制数呢?
我们先来看,如果我们想要把一个整数转化成一个十进制数组,也就是把整数的每个数字分离出来,存储到一个数组中,例如,整数123转化成数组{1, 2, 3},应该怎么来实现呢?
我们可以如下图所示,循环处理。每次对整数a除10求余,余数放入数组中,商重新赋值给a,这样操作之后,就相当于将a的最后一位数字剥离出来放入数组,并且将a的最后一位数字从a中的移除。继续上述除10求余的操作,直到a为零后结束。此时,整数中的所有的数字就都分离出来,并且放入了数组。
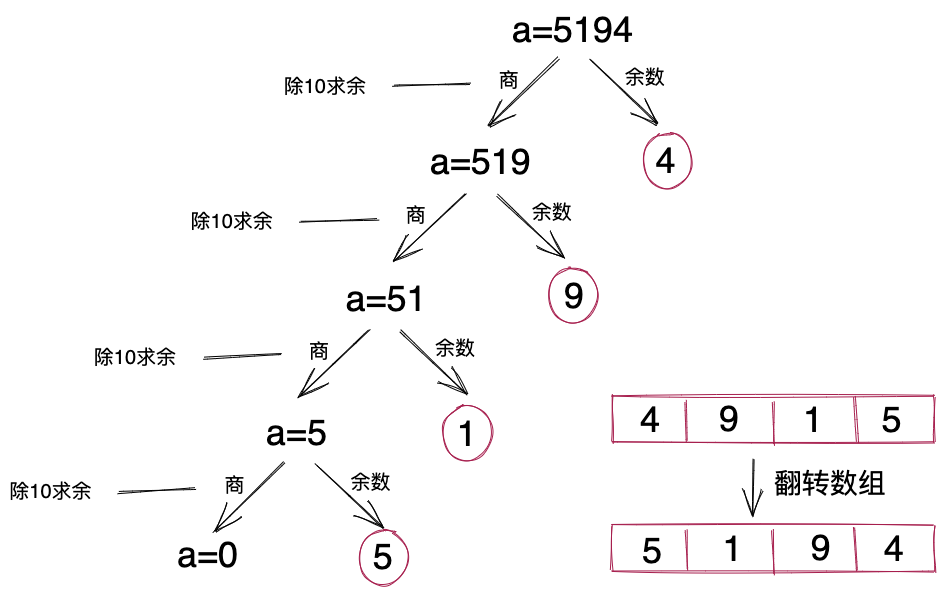
如果用代码将上述计算过程实现出来,就是下面这样子。
//a=5194 => {5,1,9,4}
public int[] convertToDecimalArray(int a) {
int[] arr = new int[10]; //int类型最大2147483647,10位数
int i = 0;
while (a != 0) {
arr[i] = a%10; //余数放入数组 {4,9,1,5}
a = a/10; //商重新赋值给a
i++;
}
swap(arr, i); //将{4,9,1,5}翻转为{5,1,9,4}
return arr;
}
public void swap(int []arr, int n) {
int i = 0;
int j = n-1;
while (i < j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
i++;
j--;
}
}
借助整数转化成十进制数组的方法,我们将整数转化成二进制数组。我们每次拿a除2求余,余数放入数组,商重新赋值给a,重复这个操作,直到a为零后结束,此时,数组中存储的就是整数的二进制数组了。计算过程举例如下。
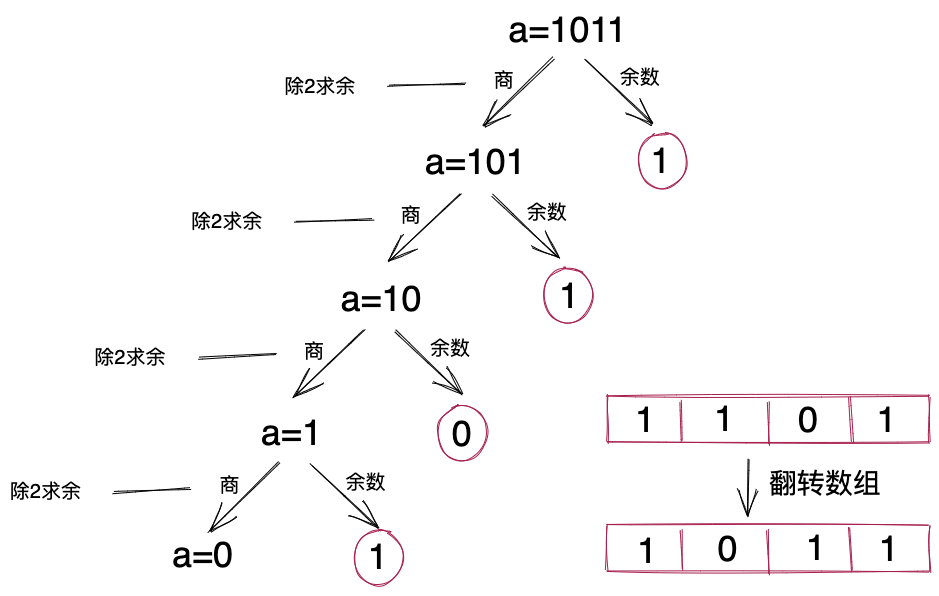
如果用代码将上述计算过程实现出来,就是下面这个样子。
//a=1011(二进制表示) => {1,0,1,1}
public int[] convertToBinaryArray(int a) {
int[] arr = new int[32]; //int型数据32位
int i = 0;
while (a != 0) {
arr[i] = a%2; //余数放入数组 {1,1,0,1}
a = a/2; //商重新赋值给a
i++;
}
//swap()函数的代码实现见上一段代码
swap(arr, i); //将{1,1,0,1}翻转为{1,0,1,1}
return arr;
}
刚刚我们讲的是,将十进制整数转换成二进制数组,反过来,二进制数组也可以转化成十进制整数。转化的其中一种方法,如下图所示,将每一位与其对应的权值相乘,得到的结果加起来,就是最终的十进制整数。

我们将上述计算方法,用代码实现出来,就是下面这样子。
// {1, 0,1, 1} -》1011(二进制表示),k=4表示二进制位个数
public int convertToDecimal(int[] binaryArr, int k) {
int a = 0;
int weight = 1;
for (int i = k-1; i >=0; --i) {
a += binaryArr[i] * weight;
weight *= 2;
}
return a;
}
当然,将二进制数组转换为十进制整数还有其他方法,如下图所示。从高位到低位,每次先将a乘以2,再取出数组中的一个数,加到a中。循环直到数组中的所有的数都加到a中结束。此时,a中存储的就是二进制数组对应的十进制整数。
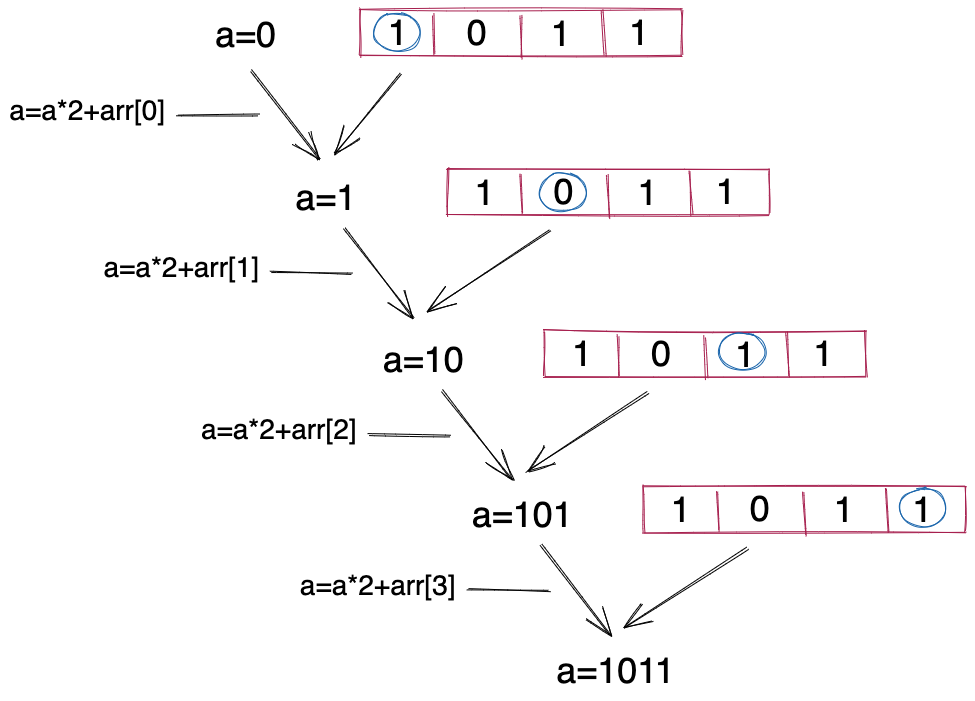
同样,我们将上述计算方法,用代码实现出来,就是下面这样子。
// {1, 0, 1, 1} -》1011(二进制表示),k=4表示二进制位个数
public int convertToDecimal2(int[] binaryArr,int k) {
int a = 0;
for (int i = 0; i < k; ++i) {
a = a*2 + binaryArr[i];
}
return a;
}
前面讲了十进制和二进制,实际上,比较常用的进制还有八进制和十六进制。八进制中每位的数字只能是0~7,十六进制中每位的数字可以是0~9、A、B、C、D、E、F。其中A~F分别对应10~15。为了区分八进制、十六进制与十进制,我们在八进制数据前面加0,在十六进制数据前面加0X或0x。举例如下所示。
int x = 12; //十进制
int y = 012; //八进制
int z = 0x12; //十六进制
System.out.println(""+x); //输出12
System.out.println(""+y); //输出10
System.out.println(""+z); //输出18
八进制跟十进制以及十六进制跟十进制的转换方法,与二进制跟十进制的转换方法类似,这里就不重复介绍了。当然,我们也可以从二进制转化为八进制和十进制。转换方法如下图举例所示。三位二进制数转化成一位八进制数,四位二进制数转换为一位十六进制数。

二、如何在计算机中表示整数:补码
刚刚我们都是拿正数来举例讲解,从讲解中,我们可以发现,正数的二进制表示是比较简单的,那负数在计算机中如何呢?
计算机并没有专门的硬件来存储数字的正负号,它只能识别0、1这样的二进制数。所以,计算机使用一串二进制数的最高位作为符号位,其余位作为数值位。符号位为0表示正数,符号位为1表示负数。我们拿长度为1个字节的byte类型数据和长度为4字节的int类型数据来举例,如下图所示。
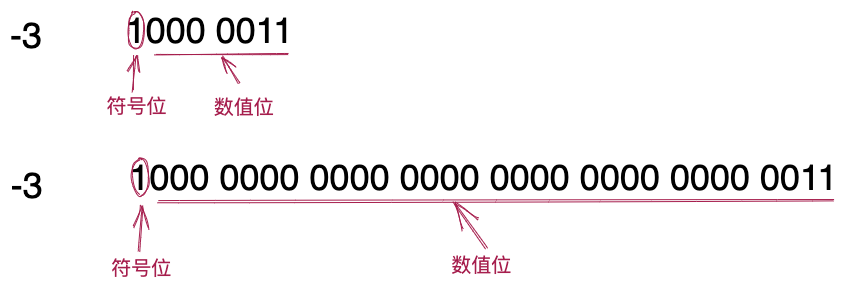
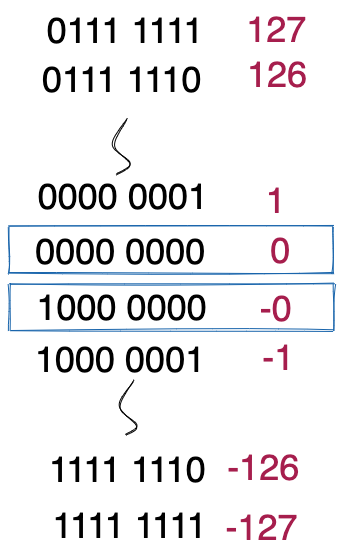
以上二进制表示法叫做原码表示法。在这种表示法中,对于长度为1个字节的byte类型的数据来说,取值范围是-127(1111 1111十六进制为0xFF)到127(0111 1111十六进制为0x7F)。比较特殊的是,0有两种表示方法+0(0000 0000)和-0(1000 0000)。
原码表示法简单直接,容易理解,但计算机并不是用原码来存储整数的。原因是使用原码表示整数,加法运算比较简单,但减法运算比较复杂,需要设计有别于加法的新的电路来实现。对于加法运算,例如3+5,表示成二进制原码(假设数据类型是byte,长度为1字节)为:0000 0011 + 0000 0101,我们只要像十进制加法运算一样,从低位向高位逐位相加逢二进一即可。如下图所示。但对于减法运算,例如5-3,如果想要复用加法电路,我们可以将其转化为:5+(-3),表示成二进制原码为:0000 0101+1000 0011,如果不区分符号位,继续按照加法的逻辑来运算,得到的结果为:1000 1000,也就是-8,显然结果是不对。如果我们区分符号位,那计算逻辑就复杂了很多,需要实现新的电路来实现正数+负数这种运算,也就是减法运算。
于是,聪明的科学家发明了一种新的整数的二进制表示法:补码表示法。利用补码,减法可以转换为加法,利用同一套电路来实现。
正数的补码跟原码相同。负数的补码是在原码的基础上先求反码,然后再+1。反码的意思是在原码的基础上,符号位不变,数值位按位取反。我们举个例子来解释一下,如下所示。
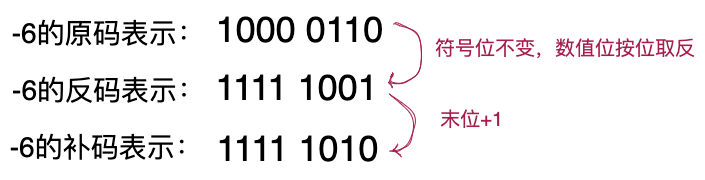
补码跟原码虽然有一定的关系,但它们是两套不同的二进制编码方式。在补码表示法中,有两个比较特殊的地方。其一是,0不再像原码那样有+0和-0的区分,-0没有对应的补码;其二是,对于长度为n(n个二进制位)的数据类型,最高位为1、数值位全为0的二进制数为-2^n的补码,此补码没有对应的原码。例如,对于byte类型,1000 0000为-128的补码, 没有对应的原码。实际上,我们也可以理解为,把-0的补码挪做去表示-128了。所以,对于长度为n(n个二进制位)的数据类型,原码的表示范围是[-2^(n-1)+1, 2(n-1)-1],而补码的表示范围是[-2(n-1), 2^(n-1)-1]。补码表示范围比原码表示范围大1。

了解了补码的编码方式之后,我们来看下如何用补码实现加减法。
因为正数的补码跟原码相同,所以,加法的运算逻辑不变,仍然是按位求和,逢二进一。对于减法,例如5-3,表示为加法就相当于:5+(-3),用补码表示就是:0000 0101+1111 1101(假设数据类型为byte,长度为1个字节),对于补码的加法,计算机不单独区分符号位和数值位,所有的二进制位一把梭,一律按照加法的运算逻辑来运算,如下图所示,得到的结果为:1 0000 0010,最前面的1溢出,被截断丢弃,所以最终结果为:0000 0010,也是补码表示,对应的整数值为2。
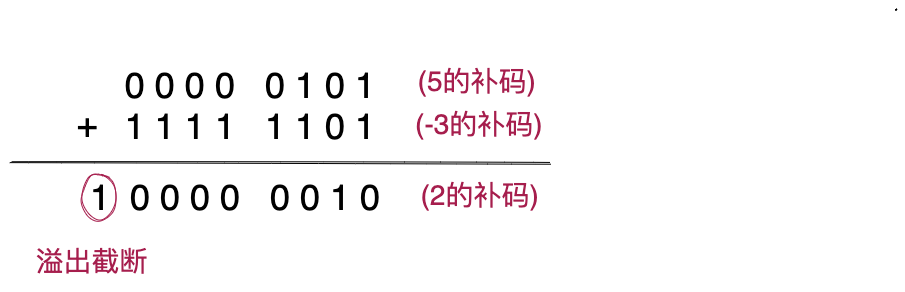
前面我们讲到,对于长度为1个字节的byte类型,在补码表示法中,-0的补码(1000 0000)挪做表示-128。这种安排并不是随意的,而是因为这样做,正好满足刚刚讲的补码的减法运算规则。例如5-128,表示成加法为:5+(-128),用补码表示为:0000 0101+1000 0000,逐位相加,最终结果为:1000 0101,正好为-123的补码。
你可能会说,把-0的补码挪作表示-128,那5-0这样的式子如何计算呢?在补码表示中,0不分正负,换种说法,+0、-0的补码都一样,都是0000 0000。所以,我们仍然可以将5-0转化为5+(-0)来计算。
接下来,我们通过理论分析,证明补码运算的正确性。
补码的加法运算(两个正数相加)的正确性不言而喻,因为两加数都为正数,正数的补码跟原码相同,加法操作就是普通的按位求和,逢二进一。我们重点来看补码的减法运算(两个正数相减)的正确性。我们拿长度为1个字节的byte类型的数据来举例讲解。
我们先来看两个非常重要的前置知识点。
1)如果两数a、b相加的结果c超过127,也就是,c包含9位二进制位,最高位是1。那么,c的高位溢出,只保留低8位的值。这个操作就相当于拿c跟2^8求模。
2)一个负数的补码和这个数的绝对值的原码按位相加(不区分处理符号位),得到的结果为2^8。比如,-10的绝对值的原码为0000 1010,-10的补码为1111 0110,不区分处理符号位,两数相加为:1 0000 0000,正好为28。也就是说,如果x是一个负数,假设其补码为y,那么-x+y=28,那么y=28+x。也就是说,负数x的补码为28+x。
有了这两个前置知识,我们再来看减法操作。我们分两种情况来分析。
1)情况一:a-b=c,c>=0(a、b都是正数)。
因为a-b>=0,所以,a-b=a-b+28,毕竟多加的28会溢出被截断。从而可以推导出:a-b=a-b+28=c,稍微转换一下,也就是:a-b=a+(28-b)=c。我们分析式子中的后面一个等式a+(28-b)=c,其中,a就是a的补码,28-b就是-b的补码(根据前置知识),c就是c的补码。所以,当我们要计算a-b时,我们只需要将a和-b表示成补码,就变成了两个补码的加法操作。推导过程如下图所示。
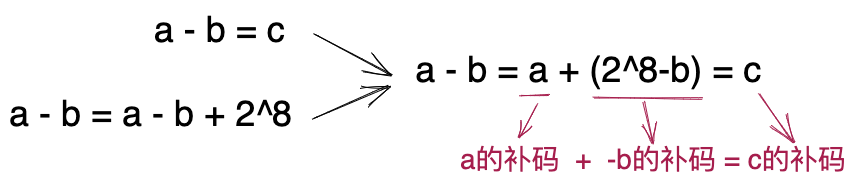
2)情况二:a-b=c,c<0(a、b都是正数)。
因为a-b<0,所以,a-b+2^8会是一个正数。因此,a-b != a-b+28。不过,我们可以得到另一个等式:a-b+28=c+28,进一步转化为:a+(28-b)=2^8+c。也就是,a的补码加上-b的补码等于c的补码。当我们要计算a-b时,我们就可以转化成a的补码加上-b的补码,最终得到的结果就是c的补码。推导过程如下图所示。
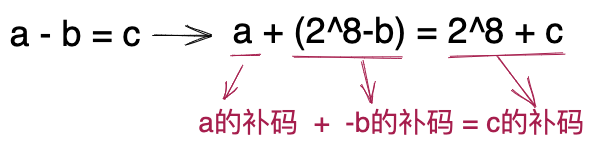
以上利用补码将减法转换为加法运算的正确性的证明比较复杂,如果实在看不懂,可以暂时不用深究。至此,我们已经掌握了整数在计算机中的表示(或存储)方法:补码。接下来,我们再来看两个补码知识点的应用:溢出和自动类型转换。
1)溢出
下面这段代码输出是什么值?
int a = 2147483647; //int类型的最大值0x7fffffff
int b = 1;
int c = a + b;
System.out.println(c);
答案是-2147483648。a在计算机中使用补码表示,因为是正数,所以,补码跟原码相同,用十六进制表示为:0x7fffffff,b也为正数,补码用十六进制表示为:0x00000001,两数相加为0x80000000,此二进制数最高位为1,其余位为0,是特殊值-232的补码。所以,这段程序打印的结果是-232,也就是-2147483648。
如何避免计算的过程中溢出呢?有的同学像如下这样来判断,你觉得对不对呢?
public int sum(int a, int b) {
if (a+b > Integer.MAX_VALUE) { //Integer.MAX_VALUE=2147483647
throw new RuntimeException("Overflow");
}
return a+b;
}
答案是不对的,因为当a+b结果大于2147483647时,就会溢出截断,截断后的值仍然小于2147483647,所以,这个函数永远都不会抛出异常。正确的方法是如下所示。这里还需要考虑a和b都为负数的时候,是否和超过int的最小值(Integer.MIN_VALUE=-2147483648)。
public int sum(int a, int b) {
boolean downOverflow = a<0 && b<0 && a<Integer.MIN_VALUE-b;
boolean upOverflow = a>0 && b>0 && a>Integer.MAX_VALUE-b;
if (downOverflow || upOverflow) {
throw new RuntimeException("Overflow");
}
return a+b;
}
2)自动类型转换
当byte类型的数据,赋值给short类型变量时,会触发自动类型转换,byte类型的数据对应的二进制数,会拷贝到short类型变量的低字节中,那么short类型的变量的高字节会怎么补全?
答案是,如果byte类型的数据是正数,那么高字节用0补全,如果byte类型的数据为负数,那么高字节用1补全。这正是因为整数在计算机中是用补码来表示的。我们拿-5举例,-5对应的补码为1111 1011,当赋值给short类型的变量时,为了保证值不变,我们在高字节处补1,结果就变成了1111 1111 1111 1011,此补码对应的原码为1000 0000 0000 0101,也就是-5。这里告诉你一个从补码反推原码的小技巧:补码的补码就是原码。如果感兴趣的话,读者可以自己证明一下其正确性。
三、计算机如何操作二进制位:位运算
如何来操作一个数中的某个或某些二进制位呢? 比如,将数中的第三位二进制位取反(如果是0,则变为1;如果是1,则变为0)。
我们可以按照本节开头讲述的方法,先将这个数转化成二进制数组,数组中每一个位置存储一个二进制位,对数组元素进行操作,将操作之后的数组再转换为十进制数。这样就完成了对这个数中某个或某些二进制位的操作。但是,这样做比较繁琐,需要来回转换,执行效率不高。接下来,我们来介绍更加高效的操作二进制位的方法,那就是:位运算。
常见的位运算有与(&)、或(|)、异或(^)、取反(!)、移位。其中,前四个运算就是逐位进行逻辑运算与、或、异或、取反。逻辑运算的真值表如下所示。两个数执行位运算,就等于两个数的补码执行位运算,例如-3 & 2 = 1111 1101 & 0000 0010 = 0000 0000 = 0。
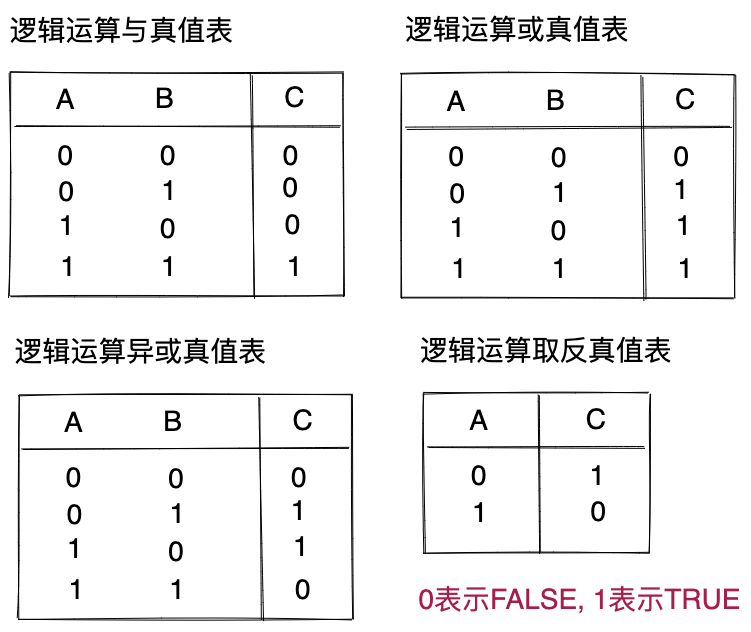
我们重点来看移位操作。移位操作分为算术位移和逻辑位移。两种运算操作的对象也是数据的补码。
逻辑位移不区分符号位,整体往左或往右移动,并且在后面或前面补全0。算术左移跟逻辑左移操作相同。对于算术右移,正数整体右移之后前面补0,负数整体右移之后前面补1。不管逻辑位移还是算术位移,超出范围的二进制位会被舍弃。

算术左移相当于乘以2,我们常常利用位运算来替代乘以2的运算,以提高运算速度。不过,当数据被左移之后,超过了可以表示的数据范围时(比如byte整型值范围为-128~127),就有可能导致数据从负数变成正数,或从正数变成负数。
算术右移相当于除以2,对于正数,不停算术右移,最终值为0。不过,对于负数来说,不停算术右移,永远都不会为0,最终值停留在-1不变。这也是开篇的代码死循环的原因。num=-3表示成补码为1111..(省略24个1)..1101,在Java中>>表示算术右移,负数前面补1,num变为所有的二进制位全为1,也就是-1的补码。如果将算术右移>>换为逻辑右移>>>,右移之后前面补0,最终num的值将会变为0。所以,循环可以结束,打印正确结果31。
public class Demo5_1 {
public static void main(String[] args) {
int count = countOneBits(-3);
System.out.println(count);
}
public static int countOneBits(int num) {
int count = 0;
while (num != 0) {
if ((num&1) == 1) count++;
num >>= 1;
}
return count;
}
}
四、课后思考题
1)编程将一个十进制数组(如{2, 3, 1})转化为十进制整数132。
2)如何证明补码的补码就是原码?