第8章 二叉树
第8章 二叉树
模板
前序遍历非递归
中序遍历非递归
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> nodes = new LinkedList<>();
Deque<TreeNode> stack = new LinkedList<TreeNode>();
TreeNode cur = root;
while(cur != null || !stack.isEmpty()){
while(cur != null){
stack.offer(cur);
cur = cur.left;
}
cur = stack.pollLast();
nodes.add(cur.val);//访问节点
cur = cur.right;
}
return nodes;
}
}
后序遍历非递归
二叉树的深度优先搜索
剑指offerⅡ47:二叉树剪枝
给定一个二叉树 根节点 root ,树的每个节点的值要么是 0,要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。
节点 node 的子树为 node 本身,以及所有 node 的后代。

class Solution {
public TreeNode pruneTree(TreeNode root) {
if(root==null){
return null;
}
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
if(root.left==null && root.right==null && root.val==0){
return null;
}
return root;
}
}
剑指offerⅠ26:树的子结构
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即A中有出现和B相同的结构和节点值。
思路:
代码:
class Solution {
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) {
return false;
}
return isMatch(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
private boolean isMatch(TreeNode A, TreeNode B) {
if (B == null) {
return true;
}
if (A == null || A.val != B.val) {
return false;
}
return isMatch(A.left, B.left) && isMatch(A.right, B.right);
}
}
剑指offerⅡ48:序列化和反序列化二叉树
方法一:层序遍历
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if(root==null)return "#";
StringBuilder sb = new StringBuilder();
Deque<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
while(!q.isEmpty()){
TreeNode node = q.poll();
if(node!=null){
sb.append(node.val+",");
q.add(node.left);
q.add(node.right);
}else{
sb.append("#,");
}
}
sb.deleteCharAt(sb.length()-1);
return sb.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data.equals("#")){
return null;
}
String[] str = data.split(",");
TreeNode root = new TreeNode(Integer.parseInt(str[0]));
Deque<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
int i=1;
while(!q.isEmpty()){
TreeNode node = q.poll();
if(!str[i].equals("#")){
node.left = new TreeNode(Integer.parseInt(str[i]));
q.offer(node.left);
}
i++;
if(!str[i].equals("#")){
node.right = new TreeNode(Integer.parseInt(str[i]));
q.offer(node.right);
}
i++;
}
return root;
}
}
方法二:先序遍历
public class Codec {
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (root == null) {
return "#";
}
String string = String.valueOf(root.val);
String left = serialize(root.left);
String right = serialize(root.right);
return string + "," + left + "," + right;
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
String[] strs = data.split(",");
int[] i = {0};
return construct(strs, i);
}
private TreeNode construct(String[] strs, int[] i) {
String str = strs[i[0]++];
if (str.equals("#")) {
return null;
}
TreeNode node = new TreeNode(Integer.valueOf(str));
node.left = construct(strs, i);
node.right = construct(strs, i);
return node;
}
}
我们需要一个下标去扫描字符串数组中的每个字符串。通常用一个整数值来表示数组的下标,但在上述代码中却定义了一个长度为1的整数数组i。这是因为construct每反序列化一个节点时下标就会增加1,并且函数的调用者需要知道下标增加了。如果函数construct的第2个参数i是整数类型,那么即使在函数体内修改i的值,修改之后的值也不能传给它的调用者。但把i定义为整数数组之后,可以修改整数数组中的数字,修改之后的数值就能传给它的调用者。
剑指offerⅡ49:从根节点到叶节点的路径之和
给定一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
class Solution {
int ans = 0;
public int sumNumbers(TreeNode root) {
dfs(root,0);
return ans;
}
public void dfs(TreeNode root, int path){
if(root == null){
return;
}
path = path * 10 + root.val;
if(root.left==null && root.right==null) {
ans = ans + path;
}
dfs(root.left, path);
dfs(root.right, path);
}
}
LC113:路径总和Ⅱ
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
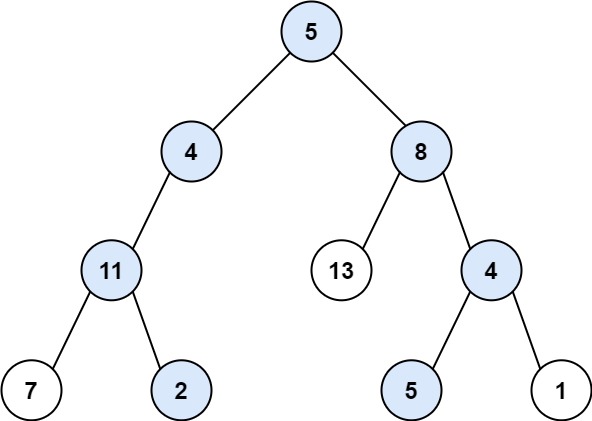
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
**思路:**DFS。
代码:
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> ans = new ArrayList<>();
dfs(root, targetSum, new ArrayList<>(), ans);
return ans;
}
private void dfs(TreeNode root, int targetSum, List<Integer> path, List<List<Integer>> ans) {
if (root == null) {
return;
}
targetSum -= root.val;
path.add(root.val);
if (root.left == null && root.right == null) {
if (targetSum == 0) {
ans.add(new ArrayList<>(path));
}
}
dfs(root.left, targetSum, path, ans);
dfs(root.right, targetSum, path, ans);
path.remove(path.size() - 1);
}
}
剑指offerⅡ50:向下的路径节点值之和
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
方法一:深度搜索
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if(root==null){
return 0;
}
int ans = rootSum(root,targetSum);
ans = ans + pathSum(root.left,targetSum);
ans = ans + pathSum(root.right,targetSum);
return ans;
}
private int rootSum(TreeNode root, int targetSum){
if(root == null){
return 0;
}
int ans = 0;
int value = root.val;
if(value==targetSum){
ans++;
}
ans = ans + rootSum(root.left,targetSum-value);
ans = ans + rootSum(root.right,targetSum-value);
return ans;
}
}
方法二:深度搜索+前缀树
class Solution {
public int pathSum(TreeNode root, int targetSum) {
Map<Integer,Integer> map = new HashMap<Integer,Integer>();
map.put(0,1);
return dfs(root,0,map,targetSum);
}
private int dfs(TreeNode root, int path, Map<Integer,Integer> map, int targetSum){
if(root==null){
return 0;
}
path = path + root.val;
int count = map.getOrDefault(path-targetSum,0);
map.put(path,map.getOrDefault(path,0)+1);//这里注意要后加入path,与前一个语句不能互换位置
count = count + dfs(root.left,path,map,targetSum);
count = count + dfs(root.right,path,map,targetSum);
//我的理解:map是"传引用"(实际上也是传值),回溯的时候需要手动修改;只有基本类型的数据在返回上一层才会恢复原来的值。
map.put(path,map.get(path)-1);
return count;
}
}
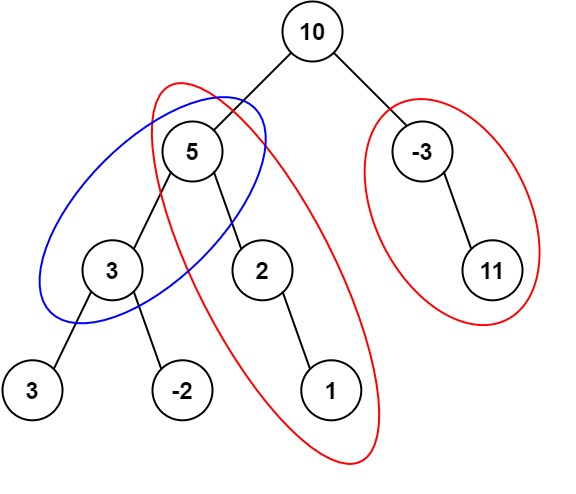
利用前缀树。加入有如下路径1-3-6-9,targetSum=9。
即将访问元素6时,此时此时path=1+3+6=10,前缀和为{0,1,4}。path-target=1,前缀和中存在1。
即将访问元素9时,此时path=1+3+6+9=19,前缀和为{0,1,4,10}。path-target=10,前缀和中存在10。
这道题是计算数量,但是如果要打印路径,利用前缀和应该这么去做:以即将访问元素6为例。
剑指offerⅡ51:节点值之和最大的路径
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给定一个二叉树的根节点 root ,返回其 最大路径和,即所有路径上节点值之和的最大值。
class Solution {
int ans = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
dfs(root);
return ans;
}
//root节点能为父节点贡献的最大路径。
private int dfs(TreeNode root){
if(root == null){
return 0;
}
//计算当前节点的左右孩子对自身的贡献left和right
int left = dfs(root.left);
int right = dfs(root.right);
// 更新最大值,就是当前节点的val 加上左右节点的贡献。
ans = Math.max(ans, root.val + left + right);
// 计算当前节点能为父亲提供的最大贡献
int max = Math.max(left, right) + root.val;
//如果该贡献为负,则应舍去
return max > 0 ? max : 0;
}
}
LC101:对称二叉树
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
class Solution {
public boolean isSymmetric(TreeNode root) {
return check(root, root);
}
private boolean check(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
} else if (p == null || q == null) {
return false;
}
return p.val == q.val && check(p.right, q.left) && check(p.left, q.right);
}
}
LC114:二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
方法一:先序遍历和展开同步进行
**思路:**由于将节点展开之后会丢失子节点的信息,所以如果先先序遍历,存储所有节点之后再连成链表,这时就是两步了。之所以会在破坏二叉树结构之后才丢失子节点的信息是因为在对左子树进行遍历时,没有存储右子节点的信息,在遍历完左子树之后才获得右子节点的信息。只要对前序遍历进行修改,在遍历左子树之前就获得左右子节点的信息,并存入栈内,子节点的信息就不会丢失,就可以将前序遍历和展开为单链表同时进行。
该做法不适用于递归实现的前序遍历,只适用于迭代实现的前序遍历。修改后的前序遍历的具体做法是,每次从栈内弹出一个节点作为当前访问的节点,获得该节点的子节点,如果子节点不为空,则依次将右子节点和左子节点压入栈内(注意入栈顺序)。
展开为单链表的做法是,维护上一个访问的节点 prev,每次访问一个节点时,令当前访问的节点为 curr,将 prev 的左子节点设为 null 以及将 prev 的右子节点设为 curr,然后将 curr 赋值给 prev,进入下一个节点的访问,直到遍历结束。需要注意的是,初始时 prev 为 null,只有在 prev 不为 null 时才能对 prev 的左右子节点进行更新。
但是这种方法的空间复杂度仍然为O(n)
class Solution {
public void flatten(TreeNode root) {
if (root == null) {
return;
}
Deque<TreeNode> stack = new LinkedList<>();
stack.add(root);
TreeNode pre = null;
while (!stack.isEmpty()) {
TreeNode cur = stack.removeLast();
if (pre != null) {
pre.left = null;
pre.right = cur;
}
if (cur.right != null) {
stack.add(cur.right);
}
if (cur.left != null) {
stack.add(cur.left);
}
pre = cur;
}
}
}
方法二:寻找前驱节点
**思路:**注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空,则该节点不需要进行展开操作。如果一个节点的左子节点不为空,则该节点的左子树中的最后一个节点被访问之后,该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点,也是该节点右子节点的前驱节点。因此,问题转化成寻找该节点的右子节点的前驱节点。
具体做法是,对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束。
class Solution {
public void flatten(TreeNode root) {
TreeNode cur = root;
while (cur != null) {
if (cur.left != null) {
TreeNode next = cur.left;
TreeNode pre = next;
while (pre.right != null) {
pre = pre.right;
}
pre.right = cur.right;
cur.right = next;
cur.left = null;
}
cur = cur.right;
}
}
}
LC226:二叉树镜像
递归:
class Solution {
public TreeNode mirrorTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode left = mirrorTree(root.left);
TreeNode right = mirrorTree(root.right);
root.right = left;
root.left = right;
return root;
}
}
栈:
队列:
二叉搜索树
剑指offerⅡ52:展平二叉搜索树
给你一棵二叉搜索树,请 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
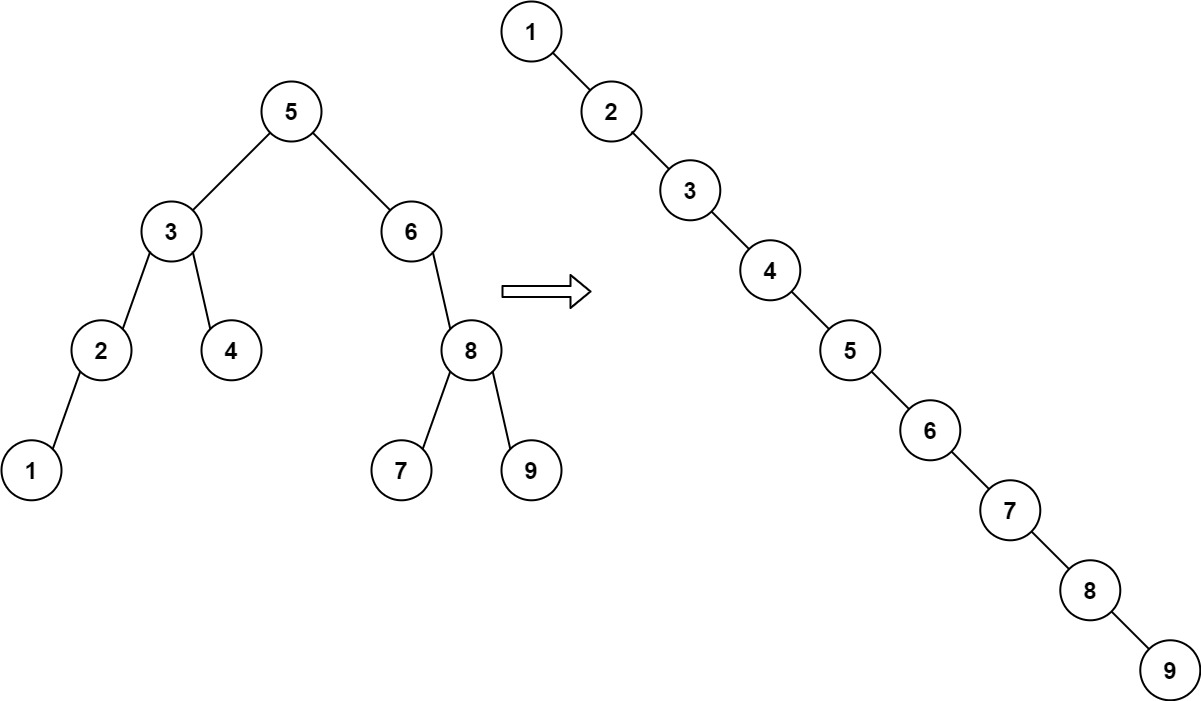
非递归(在中序遍历的过程中改变节点指向):
class Solution {
public TreeNode increasingBST(TreeNode root) {
TreeNode cur = root;
TreeNode first = null;
TreeNode prev = null;
Deque<TreeNode> stack = new LinkedList<>();//双端队列作为栈
while(cur!=null || !stack.isEmpty()){
while(cur!=null){
stack.offer(cur);
cur=cur.left;
}
cur=stack.pollLast();
//以下是访问cur节点
if(prev==null){
first=cur;
}else{
prev.right=cur;
}
cur.left=null;
prev=cur;
//以上是访问cur节点
cur=cur.right;
}
return first;
}
}
另一种迭代方法(先迭代遍历,再连节点):先中序遍历一遍在list中存储节点,再对list做一遍遍历,将这些节点用right连起来,其中left都为null。
递归(在中序遍历的过程中改变节点指向):
class Solution {
TreeNode cur;
public TreeNode increasingBST(TreeNode root) {
cur = new TreeNode(-1);
TreeNode temp = cur;
dfs(root);
return temp.right;
}
private void dfs(TreeNode root){
if(root == null){
return;
}
dfs(root.left);
cur.right=root;
root.left=null;
cur=root;
dfs(root.right);
}
}
另一种递归方法(先递归遍历,再连节点)。
剑指offerⅡ53:二叉搜索树的下一个节点
给定一棵二叉搜索树和其中的一个节点 p ,找到该节点在树中的中序后继。如果节点没有中序后继,请返回 null 。
节点 p 的后继是值比 p.val 大的节点中键值最小的节点,即按中序遍历的顺序节点 p 的下一个节点。
方法一:时间复杂度的解法
中序遍历解决问题。但是对于这个题不能这么做,时间复杂度很高。
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
Deque<TreeNode> stack = new LinkedList<>();
boolean found = false;
while(root!=null || !stack.isEmpty()){
while(root!=null){
stack.offer(root);
root=root.left;
}
root=stack.pollLast();
if(found){//先弹出root,再判断之前是否找到,如果找到了root,弹出节点就是被找节点的下一个节点
break;
}
if(p==root){
found=true;
}
root=root.right;
}
return root;
}
}
方法二:时间复杂度的解法
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
TreeNode ans = null;
while(root!=null){
if(p.val>=root.val){
root=root.right;
}else{
ans=root;
root=root.left;
}
}
return ans;
}
}
剑指offerⅡ54:所有大于等于节点的值之和
给定一个二叉搜索树,请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
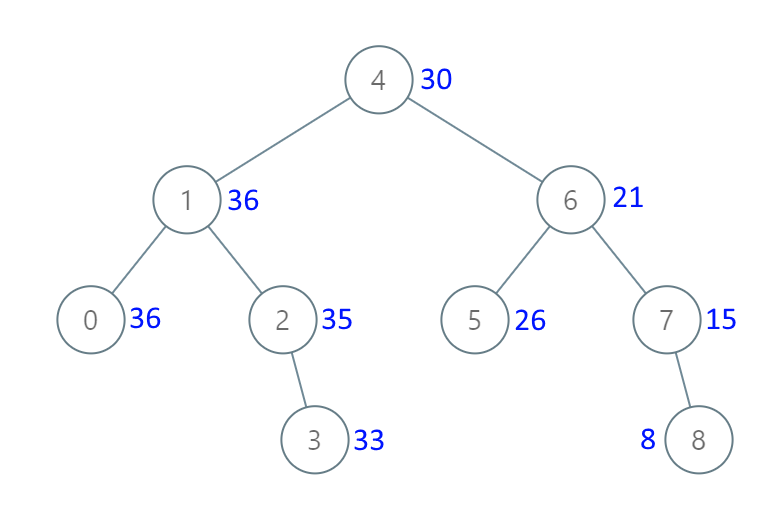
方法一:递归法
二叉搜索树正向中序遍历是从小到大,逆向中序遍历是从大到小,本题应用逆向中序遍历,统计大于等于某个节点的所有节点值之和,可以省去很多重复步骤。
class Solution {
private int sum=0;
public TreeNode convertBST(TreeNode root) {
dfs(root);
return root;
}
private void dfs(TreeNode root){
if(root==null){
return;
}
dfs(root.right);
sum+=root.val;
root.val=sum;
dfs(root.left);
}
}
方法二:非递归
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode cur = root;
Deque<TreeNode> stack = new LinkedList<TreeNode>();
while(cur!=null || !stack.isEmpty()){
while(cur!=null){
stack.offer(cur);
cur=cur.left;
}
stack.pollLast();
sum+=cur.val;
cur.val=sum;
cur=cur.right;
}
return root;
}
}
剑指offerⅡ55:二叉搜索树迭代器
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
class BSTIterator {
Deque<TreeNode> stack;
TreeNode cur;
public BSTIterator(TreeNode root) {
stack = new LinkedList<TreeNode>();
cur = root;
}
public int next() {
while(cur!=null){
stack.offer(cur);
cur=cur.left;
}
cur=stack.pollLast();
int val=cur.val;
cur=cur.right;
return val;
}
public boolean hasNext() {
return cur!=null || !stack.isEmpty();
}
}
剑指offerⅡ56:二叉搜索树中两个节点的值之和
给定一个二叉搜索树的 根节点 root 和一个整数 k , 请判断该二叉搜索树中是否存在两个节点它们的值之和等于 k 。假设二叉搜索树中节点的值均唯一。
方法一:利用哈希表,空间复杂度为O(n)
中序递归
class Solution {
Set<Integer> set = new HashSet<Integer>();
public boolean findTarget(TreeNode root, int k) {
return dfs(root,k);
}
private boolean dfs(TreeNode root, int k){
if(root==null){
return false;
}
boolean left = dfs(root.left,k);
if(set.contains(k-root.val)) {
return true;
}
set.add(root.val);
boolean right = dfs(root.right,k);
return left||right;
}
}
递归比非递归耗时更长,因为有大量的子树的逻辑合并过程,而在非递归算法是不存在这些步骤的。
中序非递归
class Solution {
Set<Integer> set = new HashSet<Integer>();
public boolean findTarget(TreeNode root, int k) {
Deque<TreeNode> stack = new LinkedList<TreeNode>();
while(root!=null || !stack.isEmpty()){
while(root!=null){
stack.offer(root);
root=root.left;
}
root=stack.pollLast();
if(set.contains(k-root.val)){
return true;
}
set.add(root.val);
root=root.right;
}
return false;
}
}
方法二:双指针,空间复杂度为O(h)
class BSTNext{
TreeNode cur;
Deque<TreeNode> stack = new LinkedList<TreeNode>();
public BSTNext(TreeNode root){
cur=root;
}
public int next(){
while(cur!=null){
stack.offer(cur);
cur=cur.left;
}
cur=stack.pollLast();
int val = cur.val;
cur=cur.right;
return val;
}
}
class BSTPrev{
TreeNode cur;
Deque<TreeNode> stack = new LinkedList<TreeNode>();
public BSTPrev(TreeNode root){
cur=root;
}
public int prev(){
while(cur!=null){
stack.offer(cur);
cur=cur.right;
}
cur=stack.pollLast();
int val = cur.val;
cur=cur.left;
return val;
}
}
class Solution {
public boolean findTarget(TreeNode root, int k) {
BSTNext bstnext = new BSTNext(root);
BSTPrev bstprev = new BSTPrev(root);
int next = bstnext.next();
int prev = bstprev.prev();
while(next!=prev){
if(next+prev==k){
return true;
}else if(next+prev>k){
prev=bstprev.prev();
}else{
next=bstnext.next();
}
}
return false;
}
}
代码面试指南:找到搜索二叉树中两个错误的节点
一棵二叉树原本是搜索二叉树,但是其中有两个节点调换了位置,使得这棵二叉树不再是搜索二叉树,请按升序输出这两个错误节点的值。(每个节点的值各不相同)
搜索二叉树:满足每个节点的左子节点小于当前节点,右子节点大于当前节点。
样例1图
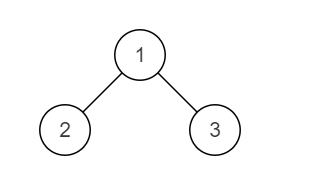
样例2图
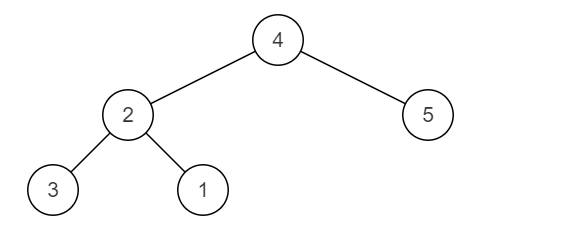
数据范围:3<=n<=100000,节点上的值满足 1<=val<=n ,保证每个value各不相同。
import java.util.*;
//节点类
public class Node{
int val;
Node left;
Node right;
Node(int value){
this.val = value;
}
}
//题解
public class Solution{
public int[] findError(Node head){
//write code here
int[] err = new int[2];
Node pre = null;
Stack<Node> stack = new Stack<Node>();
while(!stack.isEmpty() || head != null){
if(head != null){
stack.push(head);
head = head.left;
}
else{
head = stack.pop();
if(pre != null && pre.val > head.val){
err[1] = err[1] == 0 ? pre.val : err[1];
err[0] = head,val;
}
pre = head;
head = head.right
}
}
return err;
}
}
TreeSet和TreeMap的应用
剑指offerⅡ57:值和下标之差都在给定范围内
在
HashSet和HashMap中查找、添加和删除操作的时间复杂度都是,非常高效。缺点是:哈希表只能根据键查找,只能判断该键是否存在。如果需要根据数值大小查找,比如查找数据集合中比某个值大的所有数字中最小的一个,哈希表就无能为力了。此时应该用TreeSet或者TreeMap。给你一个整数数组
nums和两个整数k和t。请你判断是否存在 两个不同下标i和j,使得abs(nums[i] - nums[j]) <= t,同时又满足abs(i - j) <= k。如果存在则返回
true,不存在返回false。
方法一:暴力解法,双层循环。
方法二:时间复杂度为的解法
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
TreeSet<Long> set = new TreeSet<>();
for(int i=0;i<nums.length;i++){
Long lower = set.floor((long)nums[i]);//找到小于等于nums[i]的最大值
if(lower!=null && nums[i]-lower<=t){
return true;
}
Long upper = set.ceiling((long)nums[i]);//找到大于等于nums[i]的最小值
if(upper!=null && upper-nums[i]<=t){
return true;
}
set.add((long)nums[i]);
if(i>=k){
set.remove((long)nums[i-k]);
}
}
return false;
}
}
方法三:时间复杂度为O(n)的解法
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
Map<Integer,Long> buckets = new HashMap<>();//桶的id-值的大小
int bucketSize = t+1;
for (int i=0;i<nums.length;i++){
int id = getBucketId(nums[i],bucketSize);
if(buckets.containsKey(id)
|| (buckets.containsKey(id-1) && nums[i]-buckets.get(id-1)<=t)
|| (buckets.containsKey(id+1) && buckets.get(id+1)-nums[i]<=t)){
return true;
}
buckets.put(id,(long)nums[i]);
if(i>=k){
buckets.remove(getBucketId(nums[i-k],bucketSize));
}
}
return false;
}
private int getBucketId(int num, int bucketSize){
return num>=0 ? num/bucketSize : (num+1)/bucketSize -1;
}
}
剑指offerⅡ58:日程表
请实现一个 MyCalendar 类来存放你的日程安排。如果要添加的时间内没有其他安排,则可以存储这个新的日程安排。
MyCalendar 有一个 book(int start, int end)方法。它意味着在 start 到 end 时间内增加一个日程安排,注意,这里的时间是半开区间,即 [start, end), 实数 x 的范围为, start <= x < end。
当两个日程安排有一些时间上的交叉时(例如两个日程安排都在同一时间内),就会产生重复预订。
每次调用 MyCalendar.book方法时,如果可以将日程安排成功添加到日历中而不会导致重复预订,返回 true。否则,返回 false 并且不要将该日程安排添加到日历中。
请按照以下步骤调用 MyCalendar 类: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)
方法一:暴力
class MyCalendar {
List<int[]> events;
public MyCalendar() {
events = new ArrayList<>();
}
public boolean book(int start, int end) {
for(int[] event:events){
//start>=event[1] || end<=event[0]是满足不冲突的条件
if(start<event[1] && end>event[0]){
return false;
}
}
events.add(new int[]{start,end});
return true;
}
}
方法二:TreeMap
class MyCalendar {
private TreeMap<Integer,Integer> events;
public MyCalendar() {
events = new TreeMap<>();
}
public boolean book(int start, int end) {
Map.Entry<Integer,Integer> event = events.floorEntry(start);
if(event!=null && event.getValue()>start){
return false;
}
event = events.ceilingEntry(start);
if(event!=null && event.getKey()<end){
return false;
}
events.put(start,end);
return true;
}
}
完全二叉树
LC222:完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
解析:
首先需要明确完全二叉树的定义:它是一棵空树或者它的叶子节点只出在最后两层,若最后一层不满则叶子节点只在最左侧。
再来回顾一下满二叉的节点个数怎么计算,如果满二叉树的层数为h,则总节点数为:.那么我们来对 root 节点的左右子树进行高度统计,分别记为 left 和 right,有以下两种结果:
left == right。这说明,左子树一定是满二叉树,因为节点已经填充到右子树了,左子树必定已经填满了。所以左子树的节点总数我们可以直接得到,是 ,加上当前这个 root 节点,则正好是 。再对右子树进行递归统计。left != right。说明此时最后一层不满,但倒数第二层已经满了,可以直接得到右子树的节点个数。同理,右子树节点 加上当前这个 root 节点,总数为。再对左子树进行递归查找。
class Solution {
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
int left = depth(root.left);
int right = depth(root.right);
if (left == right) {
return countNodes(root.right) + (1 << left);
} else {
return countNodes(root.left) + (1 << right);
}
}
private int depth(TreeNode root) {
int level = 0;
while (root != null) {
root = root.left;
level++;
}
return level;
}
}
二叉树高频题
LC105,剑指offerⅠ7:重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
Map<Integer, Integer> map = new HashMap<>();
int n = preorder.length;
for (int i = 0; i < n; i++) {
map.put(inorder[i], i);
}
return build(preorder, inorder, 0, n - 1, 0, n - 1, map);
}
private TreeNode build(int[] preorder, int[] inorder, int pLeft, int pRight, int iLeft, int iRight, Map<Integer, Integer> map) {
if (pLeft > pRight) {
return null;
}
TreeNode node = new TreeNode(preorder[pLeft]);
int index = map.get(preorder[pLeft]);
int leftLength = index - iLeft + 1;
node.left = build(preorder, inorder,
pLeft + 1, pLeft + leftLength - 1,
iLeft, iLeft + leftLength - 1,
map);
node.right = build(preorder, inorder,
pLeft + leftLength, pRight,
iLeft + leftLength, iRight,
map);
return node;
}
}
LC236:二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
思路:
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return find(root, p, q);
}
private TreeNode find(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) {
return root;
}
TreeNode left = find(root.left, p, q);
TreeNode right = find(root.right, p, q);
return left == null ? right : right == null ? left : root;
}
}