第11章二分查找

Mr.Zhang大约 13 分钟

第11章二分查找

模板

y总的模板

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[left, right]被划分成[left, mid]和[mid + 1, right]时使用：
int bsearch_1(int left, int right)
{
    while (left < right)
    {
        int mid = left + right >> 1;
        if (check(mid)) right = mid;    // check()判断mid是否满足性质
        else left = mid + 1;
    }
    return left;
}
// 区间[left, r]被划分成[left, mid - 1]和[mid, r]时使用：
int bsearch_2(int left, int right)
{
    while (left < right)
    {
        int mid = left + right + 1 >> 1;
        if (check(mid)) left = mid;
        else right = mid - 1;
    }
    return left;
}

书上的模板

public int search(int[] nums, int target){
	int left = 0;
    int right = nums.length-1;
    while(left <= right){
        int mid = (left + right) / 2;
        if(nums[mid] == target){
            return mid;
        }
        
        if(nums[mid] > target){
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return -1;
}

在排序数组中的二分查找

剑指offerⅡ68：查找插入位置

给定一个排序的整数数组 nums 和一个整数目标值 target ，请在数组中找到 target ，并返回其下标。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 7
输出: 4

class Solution {
    public int searchInsert(int[] nums, int target) {
        return binarySearch(nums,0,nums.length-1,target);
    }

    private int binarySearch(int[] nums, int left, int right, int target){
        if(nums[nums.length-1]<target){
            return nums.length;//特殊情况判断
        }
        while(left < right){
            int mid = left + right >>1;
            if(nums[mid] >= target){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        return left;
    }
}

这个题不能写成right=mid-1和left=mid，因为要根据题目的要求确定区间。

剑指offerⅡ69：山峰数组的顶部

符合下列属性的数组 arr 称为 山峰数组（山脉数组） ：

arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：
- arr[0] < arr[1] < ... arr[i-1] < arr[i]
- arr[i] > arr[i+1] > ... > arr[arr.length - 1]

解法一（y总模板）：

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int left=1, right=arr.length-2;
        while(left < right){
            int mid = left + right >> 1;
            if(arr[mid]<arr[mid-1] && arr[mid]>arr[mid+1]){
                right = mid;
            }else if(arr[mid]>arr[mid-1] && arr[mid]<arr[mid+1]){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return left;
    }
}

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
        int left=1, right=arr.length-2;
        while(left < right){
            int mid = left + right + 1>> 1;
            if(arr[mid]<arr[mid-1] && arr[mid]>arr[mid+1]){
                right = mid -1 ;
            }else if(arr[mid]>arr[mid-1] && arr[mid]<arr[mid+1]){
                left = mid;
            }else{
                return mid;
            }
        }
        return left;
    }
}

最终必须返回left，因为while的条件是left<right，跳出循环结果是left。

解法二：书上的方法

没什么区别，二分范围也是[1,length-2]。

剑指offerⅡ70：排序数组中只出现一次的数字

给定一个只包含整数的有序数组 nums ，每个元素都会出现两次，唯有一个数只会出现一次，请找出这个唯一的数字。

提示:

1 <= nums.length <= 105
0 <= nums[i] <= 105

方法一：自己写的方法

class Solution {
    public int singleNonDuplicate(int[] nums) {
        int length = nums.length;
        if(length == 1){
            return nums[0];
        }
        if(nums[length-1]!=nums[length-2]){
            return nums[length-1];
        }
        if(nums[0]!=nums[1]){
            return nums[0];
        }
        int left=0, right=length-1;
        while(left<right){
            int mid=left+right>>1;
            //int mid=left+right+1>>1;
            int first=-1;
            if(nums[mid]==nums[mid+1]){
                first=mid;
            }else if(nums[mid]==nums[mid-1]){
                first=mid-1;
            }
            if(first==-1){
                return nums[mid];
            }else if(first%2==1){
                right = mid;
                //right = mid-1;
            }else{
                left = mid+1;
                //left = mid;
            }
        }
        return nums[left];
    }
}

需要注意的点：

需要考虑数组长度为1的情况;
考虑到出现一次的数字在数组的开头和末尾，这是一种特殊情况，排除以后可以计算[1,nums.length-2]的部分，访问nums[mid+1]和nums[mid-1]就不会越界;
first为相同的两个元素中第一个元素的下标

书上的方法改写为y总的模板：

剑指offerⅡ71：按权重生成随机数

给定一个正整数数组 w ，其中 w[i] 代表下标 i 的权重（下标从 0 开始），请写一个函数 pickIndex ，它可以随机地获取下标 i，选取下标 i 的概率与 w[i] 成正比。

例如，对于 w = [1, 3]，挑选下标 0 的概率为 1 / (1 + 3) = 0.25 （即，25%），而选取下标 1 的概率为 3 / (1 + 3) = 0.75（即，75%）。

也就是说，选取下标 i 的概率为 w[i] / sum(w) 。

class Solution {
    private int[] sums;
    public Solution(int[] w) {
        sums = new int[w.length];
        int total = 0, i = 0;
        for(int num:w){
            total = total + num;
            sums[i++] = total;
        }
    }
    
    public int pickIndex() {
        Random random = new Random();
        int p = random.nextInt(sums[sums.length-1]);
        int left = 0, right = sums.length-1;
        while(left<right){
            int mid = left+right>>1;
            if(sums[mid]<=p){
                left = mid+1;
            }else{
                right = mid;
            }
        }
        return left;
    }
}

思路：前缀和+二分

创建另一个和权重数组长度一样的数组sums[]，新数组的第i个数值sums[i]是权重数组前i个数字之和。

例如权重数组维[1,2,3,4]，sums为[1,3,6,10]。随机生成一个[0,10)的数，如果在[0,1)，选择下标0；如果[1,3)，选择下标1；如果[3,6)，选择下标2；如果[6,10)，选择下标3。结果如下图所示。

随机生成一个p，找到从左往右数第一个严格大于p的sums[i]，返回坐标i。

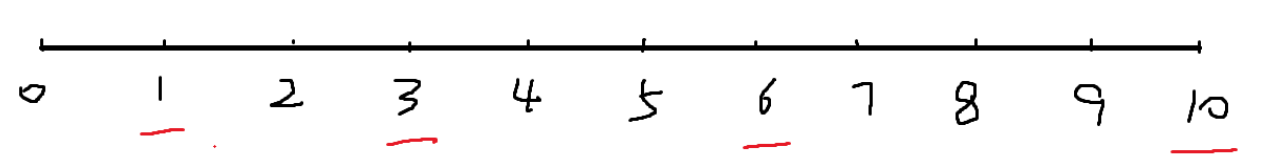
LC34：在排序数组中查找元素的第一个和最后一个位置

class Solution {
    public int[] searchRange(int[] nums, int target) {
        if(nums == null || nums.length == 0){
            return new int[]{-1, -1};
        }
        return new int[]{findStart(nums, target), findEnd(nums, target)};
    }

    private int findStart(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + right >> 1;
            if (target <= nums[mid]) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return nums[left] == target ? left : -1;
    }

    private int findEnd(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + right + 1 >> 1;
            if (nums[mid] <= target) {
                left = mid;
            } else {
                right = mid - 1;
            }
        }
        return nums[left] == target ? left : -1;
    }
}

在数值范围内二分查找

剑指offerⅡ72：求平方根

剑指offerⅡ73：狒狒吃香蕉

狒狒喜欢吃香蕉。这里有 N 堆香蕉，第 i 堆中有 piles[i] 根香蕉。警卫已经离开了，将在 H 小时后回来。

狒狒可以决定她吃香蕉的速度 K （单位：根/小时）。每个小时，她将会选择一堆香蕉，从中吃掉 K 根。如果这堆香蕉少于 K 根，她将吃掉这堆的所有香蕉，然后这一小时内不会再吃更多的香蕉，下一个小时才会开始吃另一堆的香蕉。

狒狒喜欢慢慢吃，但仍然想在警卫回来前吃掉所有的香蕉。

返回她可以在 H 小时内吃掉所有香蕉的最小速度 K（K 为整数）。

方法一：自己写的

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int max = Integer.MIN_VALUE;
        for(int pile:piles){
            max = Math.max(max,pile);
        }
        int left=1,right=max;
        while(left<right){
            int mid=left+right>>1;
            if(isEatUp(piles,h,mid)==true){
                right=mid;
            }else{
                left=mid+1;
            }
        }
        return left;
    }

    //是否能在h小时内，以速度为k吃完
    boolean isEatUp(int[] piles, int h, int k){
        int time=0;
        for(int pile:piles){
            if(pile%k==0){
                time+=pile/k;
            }else{
                time+=pile/k+1;
            }
            if(time>h){
                return false;
            }
        }
        return true;
    }
}

**方法二：书本上的方法

LC74：搜索二维矩阵Ⅰ

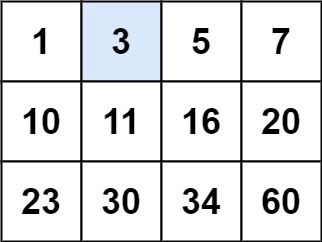
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int[] firstColumn = new int[matrix.length];
        int index = 0;
        for(int[] row:matrix){
            firstColumn[index++] = row[0];
        }
        int i = searchFirstColumn(firstColumn,target);
        int j = searchRow(matrix[i],target);
        if(matrix[i][j]==target){
            return  true;
        }
        return false;
    }

    //确定该元素出现在哪一列，返回列的下标
    private int searchFirstColumn(int[] firstColumn, int target){
        int left = 0, right = firstColumn.length-1;
        while(left<right){
            int mid = left + right + 1>> 1;
            if(target>=firstColumn[mid]){
                left = mid;
            }else{
                right = mid -1;
            }
        }
        return left;
    }

    //确定该元素在该列的哪个元素
    private int searchRow(int[] row, int target){
        int left = 0, right = row.length-1;
        while(left<right){
            int mid = left + right >> 1;
            if(target <= row[mid]){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        return left;
    }
}

LC33：搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

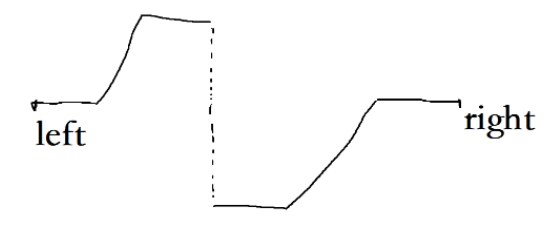
如上图所示，在算法进行过程中，left和right的相对位置共有三种可能。

对于left和right分别在两侧而言，需要判断mid在左半部分还是左半部分，接着需要判断target在mid的左侧还是右侧；
对于left和right在同一侧而言，只能有nums[mid] >= nums[left]，即只能进入第一个判断。然后需要判断target在mid的左侧还是右侧。

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + right >> 1;
            if (nums[left] <= nums[mid]) {
                if (nums[left] <= target && target <= nums[mid]) {
                    right = mid;
                } else {
                    left = mid + 1;
                }
            } else {
                if (nums[mid] < target && target <= nums[right]) {
                    //这里需要注意，必须是target > nums[mid]，这样才能有left = mid + 1;
                    //如果要用mid = left + right >> 1，那就必须有left = mid + 1;
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
        }
        return (nums[left] == target) ? left : -1;
    }
}

LC81：搜索旋转排序数组Ⅱ

已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

class Solution {
    public boolean search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + right >> 1;
            if (nums[mid] > nums[right]) {
                //mid在前半段
                if (nums[left] <= target && target <= nums[mid]) {
                    right = mid;
                } else {
                    left = mid + 1;
                }
            } else if (nums[mid] < nums[right]) {
                //mid在后半段
                if (target <= nums[right] && nums[mid] < target) {
                    left = mid + 1;
                } else {
                    right = mid;
                }
            } else {
                right--;
            }
        }
        return nums[left] == target ? true : false;
    }
}

LC154：旋转数组中的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例：

输入：numbers = [2,2,2,0,1]
输出：0

方法一（leetcode题解中的好方法）

如上图所示,是一种最朴素的情况，用二分法解决问题，mid = left + right >> 1。

如果位于mid的数小于位于right的数，那么mid一定在右半边；
如果位于mid的数大于位于right的数，那么mid一定在左半边；
如果位于mid的数等于位于right的数，那么mid要么在左半边，要么在右半边，此时可以right--；

class Solution {
    public int minArray(int[] numbers) {
        int n=numbers.length;
        return numbers[binarySearch(numbers,0,n-1)];
    }

    private int binarySearch(int[] numbers, int left, int right){
        while(left < right){
            int mid = left + right >>1;
            if(numbers[right] > numbers[mid])
                right = mid;
            else if(numbers[right] < numbers[mid])
                left = mid + 1;
            else
                right--;//其实在这一步也可以放弃二分，直接对[left,right]进行遍历，最后返回结果
        }
        return left;
    }
}

方法二（书里的方法，太过繁琐）：

如果numbers[mid]<=numbers[right]，mid在右半边；
如果numbers[mid]>=numbers[left]，mid在左半边；
但是存在一种特殊情况，把排序数组中的前0个数移到后面。针对这种情况，一旦发现数组中第一个数字小于最后一个，直接返回第一个数字；
如果right、left、mid所指的三个数字相等，则用顺序查找到最终的答案。

隐藏的二分

LC1011：在D天内送达包裹的能力

传送带上的包裹必须在 days 天内从一个港口运送到另一个港口。

传送带上的第 i 个包裹的重量为 weights[i]。每一天，我们都会按给出重量（weights）的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。

返回能在 days 天内将传送带上的所有包裹送达的船的最低运载能力。

示例：

输入：weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出：15
解释：
船舶最低载重 15 就能够在 5 天内送达所有包裹，如下所示：
第 1 天：1, 2, 3, 4, 5
第 2 天：6, 7
第 3 天：8
第 4 天：9
第 5 天：10

思路：

假设当船的运载能力为 x 时，我们可以在 days 天内运送完所有包裹，那么只要运载能力大于 x，我们同样可以在 days 天内运送完所有包裹：我们只需要使用运载能力为 x 时的运送方法即可。

这样一来，我们就得到了一个非常重要的结论：

存在一个运载能力的「下限」bottom，使得当 x≥bottom 时，我们可以在 days 天内运送完所有包裹；当 x<bottom 时，我们无法在 days 天内运送完所有包裹。

同时，bottom 即为我们需要求出的答案。因此，我们就可以使用二分查找的方法找出 bottom 的值。

在二分查找的每一步中，我们实际上需要解决一个判定问题：给定船的运载能力 x，我们是否可以在 days 天内运送完所有包裹呢？这个判定问题可以通过贪心的方法来解决：

由于我们必须按照数组 weights 中包裹的顺序进行运送，因此我们从数组 weights 的首元素开始遍历，将连续的包裹都安排在同一天进行运送。当这批包裹的重量大于运载能力 x 时，我们就需要将最后一个包裹拿出来，安排在新的一天，并继续往下遍历。当我们遍历完整个数组后，就得到了最少需要运送的天数。

我们将「最少需要运送的天数」与 days 进行比较，就可以解决这个判定问题。当其小于等于 days 时，我们就忽略二分的右半部分区间；当其大于 days 时，我们就忽略二分的左半部分区间。

细节

二分查找的初始左右边界应当如何计算呢？

对于左边界而言，由于我们不能「拆分」一个包裹，因此船的运载能力不能小于所有包裹中最重的那个的重量，即左边界为数组 weights 中元素的最大值。

对于右边界而言，船的运载能力也不会大于所有包裹的重量之和，即右边界为数组 weights 中元素的和。

我们从上述左右边界开始进行二分查找，就可以保证找到最终的答案。

代码：

class Solution {
    public int shipWithinDays(int[] weights, int days) {
        int n = weights.length;
        int left = Integer.MIN_VALUE, right = 0;
        for (int i = 0; i < n; i++) {
            left = Math.max(left, weights[i]);
            right += weights[i];
        }

        while (left < right) {
            int mid = left + right >> 1;
            int day = 1;
            int daySum = 0;
            for (int i = 0; i < n; i++) {
                if (daySum + weights[i] <= mid) {
                    daySum += weights[i];
                } else {
                    daySum = weights[i];
                    day++;
                }
            }
//两种写法，可以将注释部分替换掉上面的for循环。
//            int day = 0;
//            int i = 0;
//            while (i < n) {
//                int daySum = 0;
//                while (i < n && daySum + weights[i] <= mid) {
//                    daySum += weights[i++];
//                }
//                day++;
//            }
            if (day <= days) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

第11章 二分查找

# 第11章 二分查找

# 模板

# 在排序数组中的二分查找

# 剑指offerⅡ68：查找插入位置

# 剑指offerⅡ69：山峰数组的顶部

# 剑指offerⅡ70：排序数组中只出现一次的数字

# 剑指offerⅡ71：按权重生成随机数

# LC34：在排序数组中查找元素的第一个和最后一个位置

# 在数值范围内二分查找

# 剑指offerⅡ72：求平方根

# 剑指offerⅡ73：狒狒吃香蕉

# LC74：搜索二维矩阵Ⅰ

# LC33：搜索旋转排序数组

# LC81：搜索旋转排序数组Ⅱ

# LC154：旋转数组中的最小数字

# 隐藏的二分

# LC1011：在D天内送达包裹的能力

第11章二分查找

第11章二分查找

模板

在排序数组中的二分查找

剑指offerⅡ68：查找插入位置

剑指offerⅡ69：山峰数组的顶部

剑指offerⅡ70：排序数组中只出现一次的数字

剑指offerⅡ71：按权重生成随机数

LC34：在排序数组中查找元素的第一个和最后一个位置

在数值范围内二分查找

剑指offerⅡ72：求平方根

剑指offerⅡ73：狒狒吃香蕉

LC74：搜索二维矩阵Ⅰ

LC33：搜索旋转排序数组

LC81：搜索旋转排序数组Ⅱ

LC154：旋转数组中的最小数字

隐藏的二分

LC1011：在D天内送达包裹的能力