zhang

第1章 整数

Mr.Zhang算法整数二进制大约 6 分钟

第1章 整数

二进制

剑指offerⅡ1：整数除法

给定两个整数 a 和 b ，求它们的除法的商 a/b ，要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。

注意：

  • 整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2
  • 假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−231, 231−1]。本题中，如果除法结果溢出，则返回 231 − 1
class Solution {
    public int divide(int a, int b) {
        int MIN = Integer.MIN_VALUE, MAX = Integer.MAX_VALUE;
        if (a == MIN && b == -1) return MAX;
        int LIMIT = -1073741824; // MIN 的一半
        boolean flag = false;
        if ((a > 0 && b < 0) || (a < 0 && b > 0)) flag = true;
        if (a > 0) a = -a;
        if (b > 0) b = -b;
        int ans = 0;
        while (a <= b) {
            //这里必须是a<=b
            int k = -1, c = b;
            //这里c>LIMIT && k>LIMIT && a-c<c判定条件加不加=都可以
            while (c > LIMIT && k > LIMIT && a - c < c) {
                k = k + k;
                c = c + c;
            }
            a = a - c;
            ans = ans + k;
        }
        return flag == true ? ans : -ans;
    }
}

几个需要注意的点：

  • 因为int型中，最小的负数要比最大的负数绝对值大1，所以if(a==MIN && b==-1)return MAX；
  • a和b转换成负数来计算，如果都是正数，会有溢出的问题；
  • 需要判断c>LIMIT && k>LIMIT，判断是否超过了最小负数的一半。

剑指offerⅡ2：二进制加法

给定两个 01 字符串 a 和 b ，请计算它们的和，并以二进制字符串的形式输出。

输入为 非空 字符串且只包含数字 1 和 0。

方法一：冗长但易懂

class Solution {
    public String addBinary(String a, String b) {
        int i = a.length() - 1, j = b.length() - 1;
        StringBuilder ans = new StringBuilder();
        int carry = 0, sum;
        while (i >= 0 && j >= 0) {
            sum = getNum(a.charAt(i)) + getNum(b.charAt(j)) + carry;
            carry = sum >= 2 ? 1 : 0;
            sum %= 2;
            ans.append(sum);
            i--;
            j--;
        }
        while (i >= 0) {
            sum = getNum(a.charAt(i)) + carry;
            carry = sum >= 2 ? 1 : 0;
            sum = sum % 2;
            ans.append(sum);
            i--;
        }
        while (j >= 0) {
            sum = getNum(b.charAt(j)) + carry;
            carry = sum >= 2 ? 1 : 0;
            sum = sum % 2;
            ans.append(sum);
            j--;
        }
        if (carry == 1) {
            ans.append(carry);
        }
        return ans.reverse().toString();
    }

    private int getNum(char ch) {
        return ch - '0';
    }
}

方法二：简洁

class Solution {
    public String addBinary(String a, String b) {
        StringBuilder ans = new StringBuilder();
        int i = a.length() - 1;
        int j = b.length() - 1;
        int carry = 0;
        while (i >= 0 || j >= 0) {
            int digitA = i >= 0 ? getNum(a.charAt(i--)) : 0;
            int digitB = j >= 0 ? getNum(b.charAt(j--)) : 0;
            int sum = digitA + digitB + carry;
            carry = sum >= 2 ? 1 : 0;
            sum = sum >= 2 ? sum - 2 : sum;
            ans.append(sum);
        }
        if (carry == 1) {
            ans.append(carry);
        }
        return ans.reverse().toString();
    }

    private int getNum(char ch) {
        return ch - '0';
    }
}

剑指offerⅡ3：前n个数字二进制形式中1的个数

给定一个非负整数 n ，请计算 0 到 n 之间的每个数字的二进制表示中 1 的个数，并输出一个数组。

方法一：简单计算每个整数二进制形式中的1的个数

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n + 1];
        for (int i = 0; i < n + 1; i++) {
            int num = i;
            while (num > 0) {
                ans[i]++;
                num = (num - 1) & num;
            }
        }
        return ans;
    }
}

方法二：根据i&(i-1)计算二进制中1的个数

class Solution {
    public int[] countBits(int n) {
        int[] ans = new int[n + 1];
        for (int i = 1; i < n + 1; i++) {
            ans[i] = ans[i & (i - 1)] + 1;
        }
        return ans;
    }
}

剑指offerⅡ4：只出现1次的数字

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。

写法一（书上的写法）：

class Solution {
    public int singleNumber(int[] nums) {
        int[] bits = new int[32];
        for (int num : nums) {
            for (int i = 0; i < 32; i++) {
                //最高位到最低位
                //+的优先级高于&，所以=后面一定要加()
                bits[i] = bits[i] + ((num >> (31 - i)) & 1);
            }
        }
        int ans = 0;
        for (int i = 0; i < 32; i++) {
            ans = (ans << 1) + bits[i] % 3;
        }
        return ans;
    }
}

写法二（自己的写法，更简洁且易理解）：

class Solution {
    public int singleNumber(int[] nums) {
        int count[] = new int[32];
        for (int num : nums) {
            for (int i = 0; i < 32; i++) {
                count[i] += (num >> i) & 1;
            }
        }
        int ans = 0;
        for (int i = 0; i < 32; i++) {
           ans += (count[i] % 3) << i;
        }
        return ans;
    }
}

举一反三：输入一个整数数组，数组中只有一个数字出现了m次，其他数字都出现n次。找出唯一出现m次的数字。当然，n不能为m的倍数。

剑指offerⅡ5：单词长度的最大乘积

给定一个字符串数组 words，请计算当两个字符串 words[i] 和 words[j] 不包含相同字符时，它们长度的乘积的最大值。假设字符串中只包含英语的小写字母。如果没有不包含相同字符的一对字符串，返回 0。

示例 :

输入: words = ["abcw","baz","foo","bar","fxyz","abcdef"]
输出: 16 
解释: 这两个单词为 "abcw", "fxyz"。它们不包含相同字符，且长度的乘积最大。

方法一：哈希表记录字符串中出现的字符

class Solution {
    public int maxProduct(String[] words) {
        boolean[][] flag = new boolean[words.length][26];
        for (int i = 0; i < words.length; i++) {
            for (char ch : words[i].toCharArray()) {
                flag[i][ch - 'a'] = true;
            }
        }
        int max = 0, k;
        for (int i = 0; i < words.length; i++) {
            for (int j = i + 1; j < words.length; j++) {
                for (k = 0; k < 26; k++) {
                    if (flag[i][k] && flag[j][k] == true) {
                        break;
                    }
                }
                if (k == 26) {
                    int product = words[i].length() * words[j].length();
                    max = Math.max(product, max);
                }
            }
        }
        return max;
    }
}

方法二：整数二进制数位记录字符串出现的字符

class Solution {
    public int maxProduct(String[] words) {
        int[] flag = new int[words.length];
        int max = 0;
        for (int i = 0; i < words.length; i++) {
            for (char ch : words[i].toCharArray()) {
                flag[i] = flag[i] | (1 << (ch - 'a'));
            }
        }
        for (int i = 0; i < words.length; i++) {
            for (int j = i + 1; j < words.length; j++) {
                if ((flag[i] & flag[j]) == 0) {
                    int product = words[i].length() * words[j].length();
                    max = Math.max(max, product);
                }
            }
        }
        return max;
    }
}

LC50：Pow(x, n)

实现 pow(x, n)open in new window ，即计算 x 的 n 次幂函数。

示例1 ：

输入：x = 2.10000, n = 3
输出：9.26100

示例2 ：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

  • -100.0 < x < 100.0
  • -2^31 <= n <= 2^31-1
  • -10^4 <= x^n <= 10^4

代码：

class Solution {
    public double myPow(double x, int n) {
        if (x == 0) {
            return 0;
        }
        long b = n;
        double ans = 1;
        if (b < 0) {
            x = 1 / x;
            b = -b;
        }
        while (b > 0) {
            if ((b & 1) == 1) {
                ans = ans * x;
            }
            x = x * x;
            b = b >> 1;
        }
        return ans;
    }
}

位运算

LC89：格雷编码

n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：

  • 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
  • 第一个整数是 0
  • 一个整数在序列中出现 不超过一次
  • 每对 相邻 整数的二进制表示 恰好一位不同 ，且
  • 第一个 和 最后一个 整数的二进制表示 恰好一位不同

给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

思路：

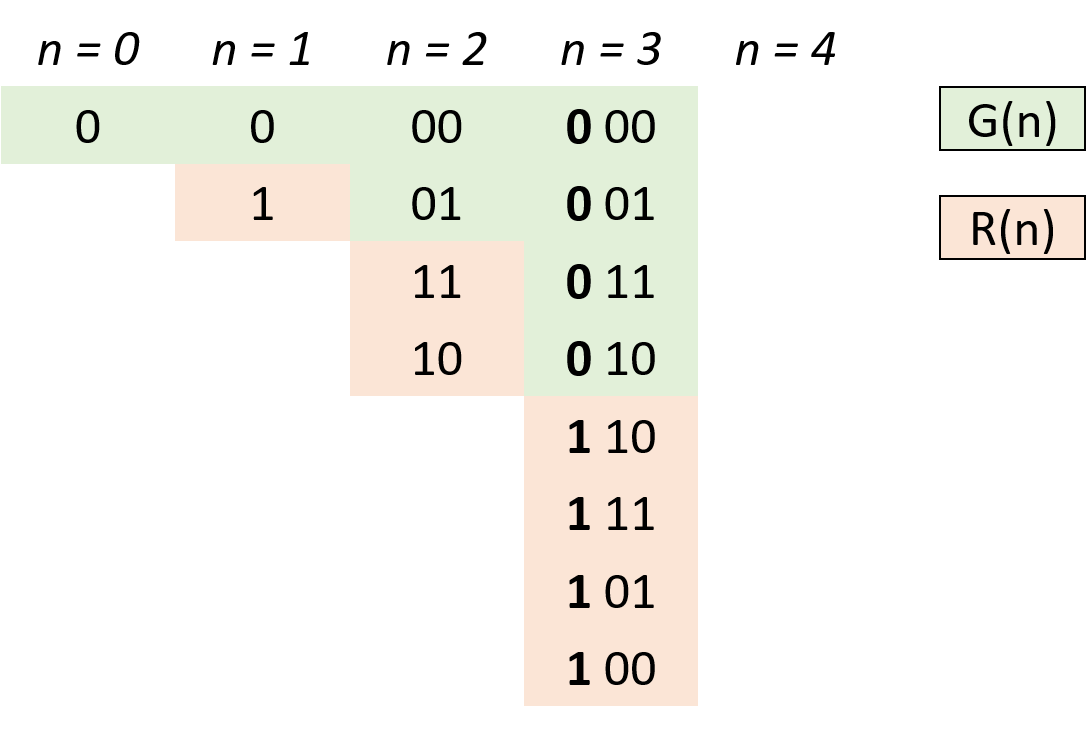
  • 设n阶格雷码集合为G(n)，则G(n+1) 阶格雷码为：
    • 给 G(n) 阶格雷码每个元素二进制形式前面添加 0，得到 G′(n)；
    • 设 G(n) 集合倒序（镜像）为 R(n)，给 R(n) 每个元素二进制形式前面添加 1，得到 R′(n)；
    • G(n+1)=G′(n)∪R′(n) 拼接两个集合即可得到下一阶格雷码。
  • 根据以上规律，可从 0 阶格雷码推导致任何阶格雷码。
  • 代码解析：
    • 由于最高位前默认为 0，因此 G′(n)=G(n)，只需在 res(即 G(n) )后添加 R′(n) 即可；
    • 计算 R′(n)：执行 head = 1 << i 计算出对应位数，以给 R(n) 前添加 1 得到对应 R′(n)；
    • 倒序遍历 res(即 G(n) )：依次求得 R′(n) 各元素添加至 res 尾端，遍历完成后 res(即 G(n+1))。
img
img
class Solution {
    public List<Integer> grayCode(int n) {
        List<Integer> ans = new ArrayList<>();
        ans.add(0);
        int position = 1;
        for (int i = 0; i < n; i++) {
            for (int j = ans.size() - 1; j >= 0; j--) {
                ans.add(ans.get(j) + position);
            }
            position <<= 1;
        }
        return ans;
    }
}

其他

Loading...
很高兴见到你
Copyright © 2022 Mr.Zhang